102. 二叉树的层序遍历
题干
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
思路
经典bfs,队列每次处理一层,将下一层节点入队
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if(!root) return res;
queue<TreeNode*> queue1;
queue1.push(root);
while(!queue1.empty()){
int size = queue1.size();
vector<int> level;
for(int i=0;i<size;i++){
TreeNode* temp = queue1.front();
level.push_back(temp->val);
queue1.pop();
if(temp->left){
queue1.push(temp->left);
}
if(temp->right){
queue1.push(temp->right);
}
}
res.push_back(level);
}
return res;
}
};
103. 二叉树的锯齿形层序遍历
题干
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -100 <= Node.val <= 100
思路
和102. 二叉树的层序遍历类似,每层放入队列时根据标识符判断是正向入队还是反向入队,这里的队列简单一点用deque双向队列表示
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
if(!root) return {};
vector<vector<int>> answer;
deque<TreeNode*> q;
q.push_back(root);
int flag = 1;
while(q.size()>0){
int len = q.size();
vector<int> temp;
if(flag>0){
for(int i=0;i<len;i++){
TreeNode* t = q.front();
temp.push_back(t->val);
q.pop_front();
if(t->left){
q.push_back(t->left);
}
if(t->right){
q.push_back(t->right);
}
}
}
else{
for(int i=0;i<len;i++){
TreeNode* t = q.back();
temp.push_back(t->val);
q.pop_back();
if(t->right){
q.push_front(t->right);
}
if(t->left){
q.push_front(t->left);
}
}
}
answer.push_back(temp);
flag = -flag;
}
return answer;
}
};
105. 从前序与中序遍历序列构造二叉树
题干
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
思路
前序遍历的第一个数为中间节点,从中序遍历找到这个数后左右划分,再找到前序遍历中对应部分便能形成两个子问题,所以dfs分治递归即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* dfs(vector<int>& preorder, vector<int>& inorder,int prestart,int preend,int instart,int inend){
if(prestart>preend){
return nullptr;
}
TreeNode* answer = new TreeNode(preorder[prestart]);
int midnum = preorder[prestart];
int pos;
for(int i=instart;i<=inend;i++){
if(inorder[i]==midnum){
pos=i;
break;
}
}
int leftsize = pos-instart;
int rightsize = inend-pos;
answer->left = dfs(preorder,inorder,prestart+1,prestart+leftsize,instart,pos-1);
answer->right = dfs(preorder,inorder,prestart+leftsize+1,preend,pos+1,inend);
return answer;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return dfs(preorder,inorder,0,preorder.size()-1,0,inorder.size()-1);
}
};
106. 从中序与后序遍历序列构造二叉树
题干
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:

输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000postorder.length == inorder.length-3000 <= inorder[i], postorder[i] <= 3000inorder和postorder都由 不同 的值组成postorder中每一个值都在inorder中inorder保证是树的中序遍历postorder保证是树的后序遍历
思路
后序遍历的最后一个数为中间节点,从中序遍历找到这个数后左右划分,再找到后序遍历中对应部分便能形成两个子问题,所以dfs分治递归即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* dfs(vector<int>& inorder, vector<int>& postorder,int istart,int iend,int pstart,int pend){
if(pend<pstart){
return nullptr;
}
int pos;
int midnum = postorder[pend];
for(int i=istart;i<iend;i++){
if(inorder[i]==midnum){
pos = i;
break;
}
}
TreeNode* answer = new TreeNode(midnum);
answer->left = dfs(inorder,postorder,istart,pos-1,pstart,pstart+pos-istart-1);
answer->right = dfs(inorder,postorder,pos+1,iend,pstart+pos-istart,pend-1);
return answer;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return dfs(inorder,postorder,0,inorder.size()-1,0,postorder.size()-1);
}
};
107. 二叉树的层序遍历 II
题干
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
示例 1:

输入:root = [3,9,20,null,null,15,7]
输出:[[15,7],[9,20],[3]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
思路
正常层序遍历,最后答案逆序即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> res;
vector<vector<int>> reverseres;
if(!root) return res;
queue<TreeNode*> qu;
qu.push(root);
while(!qu.empty())
{
vector<int> tmp;
int len=qu.size();
for(int i=0;i<len;i++){
TreeNode* node=qu.front();
qu.pop();
tmp.push_back(node->val);
if(node->left) qu.push(node->left);
if(node->right) qu.push(node->right);
}
res.push_back(tmp);
}
reverseres=res;
reverse(reverseres.begin(),reverseres.end());
return reverseres;
}
};
109. 有序链表转换二叉搜索树
题干
给定一个单链表的头节点 head ,其中的元素 按升序排序 ,将其转换为
平衡
二叉搜索树。
示例 1:
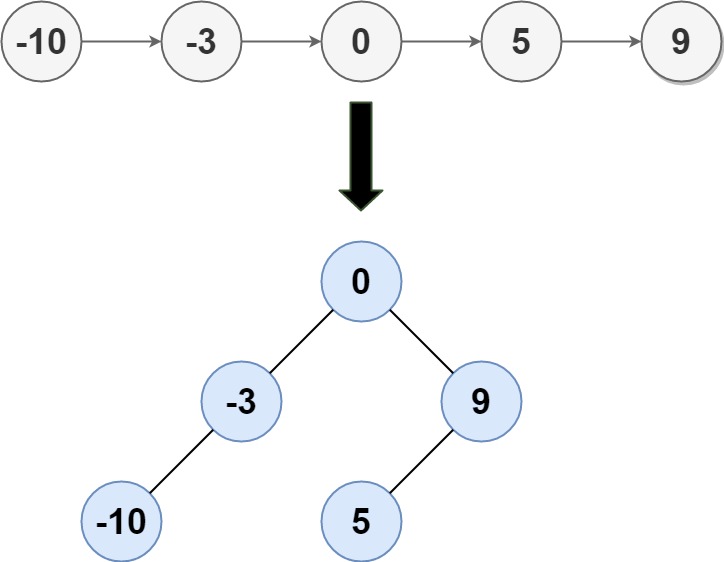
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9,-10,null,5]
解释: 一个可能的答案是[0,-3,9,-10,null,5],它表示所示的高度平衡的二叉搜索树。
示例 2:
输入: head = []
输出: []
提示:
head中的节点数在[0, 2 * 104]范围内-105 <= Node.val <= 105
思路
分支法,每次用快慢指针找到中间项slow作为当前树节点(同时记录slow前一个点),随slow左右后分割成两个新链表分别是当前树节点的左子树和右子树,代码示例中是链表递归法。另一种是先遍历链表得到vector数组,再用同样的方法分治理,因为每次取的是中间值,因此二叉搜索树的平衡性可以保证
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* dfs(ListNode* head){
if(!head){
return nullptr;
}
ListNode* dummy = new ListNode();
dummy->next = head;
ListNode* before = dummy;
ListNode* slow = head;
ListNode* fast = head;
while(fast){
fast = fast->next;
if(fast&&fast->next){
fast = fast->next;
}else{
break;
}
slow = slow->next;
before = before->next;
}
TreeNode* now = new TreeNode(slow->val);
before->next = nullptr;
ListNode* left = dummy->next;
ListNode* right = slow->next;
slow->next = nullptr;
now->left = dfs(left);
now->right = dfs(right);
return now;
}
TreeNode* sortedListToBST(ListNode* head) {
return dfs(head);
}
};
113. 路径总和 II
题干
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:

输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:

输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
思路
dfs记录路径和target值,叶子节点满足时添加路径到答案
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> answer;
vector<int> temp;
void dfs(TreeNode* root, int targetSum){
if(!root->left&&!root->right){
if(targetSum==root->val){
temp.push_back(root->val);
answer.push_back(temp);
temp.pop_back();
}
}
else{
if(root->left){
temp.push_back(root->val);
dfs(root->left,targetSum-root->val);
temp.pop_back();
}
if(root->right){
temp.push_back(root->val);
dfs(root->right,targetSum-root->val);
temp.pop_back();
}
}
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if(!root) return {};
dfs(root,targetSum);
return answer;
}
};
114. 二叉树展开为链表
题干
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [0]
输出:[0]
提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
进阶:你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
思路
dfs前向遍历,用一个dummy节点记录最终答案,temp从dummy开始每前序遍历一个向right指针添加,注意要实现原地算法前向遍历root时预先记录left和right后将root->left和root->right设置为nullptr,再dfs(left)和dfs(right)
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void flatten(TreeNode* root) {
if(!root){
return;
}
TreeNode* dummy = new TreeNode();
TreeNode* temp = dummy;
function<void(TreeNode*)> dfs = [&](TreeNode* root){
TreeNode* left = root->left;
TreeNode* right = root->right;
root->left = nullptr;
root->right = nullptr;
temp->right = root;
temp = temp->right;
if(left){
dfs(left);
}
if(right){
dfs(right);
}
};
dfs(root);
}
};
116. 填充每个节点的下一个右侧节点指针
题干
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例 1:

输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,'#' 标志着每一层的结束。
示例 2:
输入:root = []
输出:[]
提示:
- 树中节点的数量在
[0, 212 - 1]范围内 -1000 <= node.val <= 1000
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
思路
层次遍历时记录每层,对每次的节点更新right即可
代码
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
queue<Node*> queue1=queue<Node*>();
if(root==nullptr) return root;
queue1.push(root);
while(queue1.size()>0){
int levelNum = queue1.size();
Node* first = queue1.front();
queue1.pop();
levelNum--;
if(first->left!=nullptr){
queue1.push(first->left);
}
if(first->right!=nullptr){
queue1.push(first->right);
}
while(levelNum>0){
Node* second = queue1.front();
queue1.pop();
levelNum--;
if(second->left!=nullptr){
queue1.push(second->left);
}
if(second->right!=nullptr){
queue1.push(second->right);
}
first->next=second;
first = second;
}
}
return root;
}
};
117. 填充每个节点的下一个右侧节点指针 II
题干
给定一个二叉树:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL 。
初始状态下,所有 next 指针都被设置为 NULL 。
示例 1:

输入:root = [1,2,3,4,5,null,7]
输出:[1,#,2,3,#,4,5,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。序列化输出按层序遍历顺序(由 next 指针连接),'#' 表示每层的末尾。
示例 2:
输入:root = []
输出:[]
提示:
- 树中的节点数在范围
[0, 6000]内 -100 <= Node.val <= 100
进阶:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序的隐式栈空间不计入额外空间复杂度。
思路
层次遍历时记录每层,对每次的节点更新right即可
代码
/*
// Definition for a Node.
class Node {
public:
int val;
Node* left;
Node* right;
Node* next;
Node() : val(0), left(NULL), right(NULL), next(NULL) {}
Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}
Node(int _val, Node* _left, Node* _right, Node* _next)
: val(_val), left(_left), right(_right), next(_next) {}
};
*/
class Solution {
public:
Node* connect(Node* root) {
if(!root){
return nullptr;
}
queue<Node*> qu;
qu.push(root);
while(qu.size()>0){
int level_size = qu.size();
for(int i=0;i<level_size;i++){
Node* temp = qu.front();
qu.pop();
if(temp->left!=nullptr){
qu.push(temp->left);
}
if(temp->right!=nullptr){
qu.push(temp->right);
}
if(i<level_size-1){
temp->next = qu.front();
}else{
temp->next = nullptr;
}
}
}
return root;
}
};
120. 三角形最小路径和
题干
给定一个三角形 triangle ,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说,如果正位于当前行的下标 i ,那么下一步可以移动到下一行的下标 i 或 i + 1 。
示例 1:
输入:triangle = [[2],[3,4],[6,5,7],[4,1,8,3]]
输出:11
解释:如下面简图所示:
2
3 4
6 5 7
4 1 8 3
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
示例 2:
输入:triangle = [[-10]]
输出:-10
提示:
1 <= triangle.length <= 200triangle[0].length == 1triangle[i].length == triangle[i - 1].length + 1-104 <= triangle[i][j] <= 104
进阶:
- 你可以只使用
O(n)的额外空间(n为三角形的总行数)来解决这个问题吗?
思路
动态规划,对于每个层的0位置,其等于f[i][0] = f[i - 1][0] + triangle[i][0];
中间位置为f[i][j] = min(f[i - 1][j - 1], f[i - 1][j]) + triangle[i][j];
末尾位置为f[i][i] = f[i - 1][i - 1] + triangle[i][i];
代码
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int n = triangle.size();
vector<vector<int>> f(n, vector<int>(n));
f[0][0] = triangle[0][0];
for (int i = 1; i < n; ++i) {
f[i][0] = f[i - 1][0] + triangle[i][0];
for (int j = 1; j < i; ++j) {
f[i][j] = min(f[i - 1][j - 1], f[i - 1][j]) + triangle[i][j];
}
f[i][i] = f[i - 1][i - 1] + triangle[i][i];
}
return *min_element(f[n - 1].begin(), f[n - 1].end());
}
};
122. 买卖股票的最佳时机 II
题干
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
思路
贪心,每次取相邻两个后减前之差大于0的放入答案
代码
class Solution {
public:
int maxProfit(vector<int>& prices) {
int p=0;
int i;
for(i=1; i<prices.size(); ++i)
p += max(0,prices[i]-prices[i-1]);
return p;
}
};
128. 最长连续序列
题干
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
提示:
0 <= nums.length <= 105-109 <= nums[i] <= 109
思路
并查集或者哈希表。对于哈希表来说先去重放入set然后找开头元素,枚举nums[i],如果nums[i]-1不在set中则跳过,否则从nums[i]开始计数,直到nums[i]+k不在set中,更新当前答案
代码
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
unordered_set<int> num_set;
for (const int& num : nums) {
num_set.insert(num);
}
int longestStreak = 0;
for (const int& num : num_set) {
if (!num_set.count(num - 1)) {
int currentNum = num;
int currentStreak = 1;
while (num_set.count(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = max(longestStreak, currentStreak);
}
}
return longestStreak;
}
};
129. 求根节点到叶节点数字之和
题干
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:

输入:root = [1,2,3]
输出:25
解释:
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此,数字总和 = 12 + 13 = 25
示例 2:

输入:root = [4,9,0,5,1]
输出:1026
解释:
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
思路
dfs把每条路径存起来,最后求和
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int answer;
void dfs(TreeNode* root,int num){
if(!root->left&&!root->right){
answer+=num*10+root->val;
return;
}
if(root->left){
dfs(root->left,num*10+root->val);
}
if(root->right){
dfs(root->right,num*10+root->val);
}
}
int sumNumbers(TreeNode* root) {
answer = 0;
dfs(root,0);
return answer;
}
};
130. 被围绕的区域
题干
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:

输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 200board[i][j]为'X'或'O'
思路
对周围一圈的O作为起点dfs遍历将其设置为Y,最后遍历二维数组将剩余的O改为X,剩余的Y恢复为O
代码
class Solution {
public:
vector<vector<int>> dir = {{-1,0},{0,1},{1,0},{0,-1}};
void dfs(vector<vector<char>>& board,int i,int j){
if(board[i][j]=='O'){
board[i][j]='Y';
}else if(board[i][j]=='X'||board[i][j]=='Y'){
return;
}
for(int k=0;k<4;k++){
if(i+dir[k][0]>=0&&i+dir[k][0]<board.size()&&j+dir[k][1]>=0&&j+dir[k][1]<board[0].size()){
dfs(board,i+dir[k][0],j+dir[k][1]);
}
}
}
void solve(vector<vector<char>>& board) {
for(int i=0;i<board.size();i++){
dfs(board,i,0);
dfs(board,i,board[0].size()-1);
}
for(int i=0;i<board[0].size();i++){
dfs(board,0,i);
dfs(board,board.size()-1,i);
}
for(int i=0;i<board.size();i++){
for(int j=0;j<board[0].size();j++){
if(board[i][j]=='O'){
board[i][j]='X';
}
}
}
for(int i=0;i<board.size();i++){
for(int j=0;j<board[0].size();j++){
if(board[i][j]=='Y'){
board[i][j]='O';
}
}
}
}
};
131. 分割回文串
题干
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是
回文串
。返回 s 所有可能的分割方案。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
提示:
1 <= s.length <= 16s仅由小写英文字母组成
思路
本题动态规划结合dfs,先通过构建dp[i][j]动态规划判断i到j是否是回文,判断方法是边界预设好后对于剩下的值如果s[i]==s[j]则其答案等于dp[i+1][j-1]
随后用dfs每次取当前一个合适的回文串再dfs下一个回溯到末尾则添加答案
代码
class Solution {
private:
vector<vector<int>> f;
vector<vector<string>> ret;
vector<string> ans;
int n;
public:
void dfs(const string& s, int i) {
if (i == n) {
ret.push_back(ans);
return;
}
for (int j = i; j < n; ++j) {
if (f[i][j]) {
ans.push_back(s.substr(i, j - i + 1));
dfs(s, j + 1);
ans.pop_back();
}
}
}
vector<vector<string>> partition(string s) {
n = s.size();
f.assign(n, vector<int>(n, true));
for (int i = n - 1; i >= 0; --i) {
for (int j = i + 1; j < n; ++j) {
f[i][j] = (s[i] == s[j]) && f[i + 1][j - 1];
}
}
dfs(s, 0);
return ret;
}
};
133. 克隆图
题干
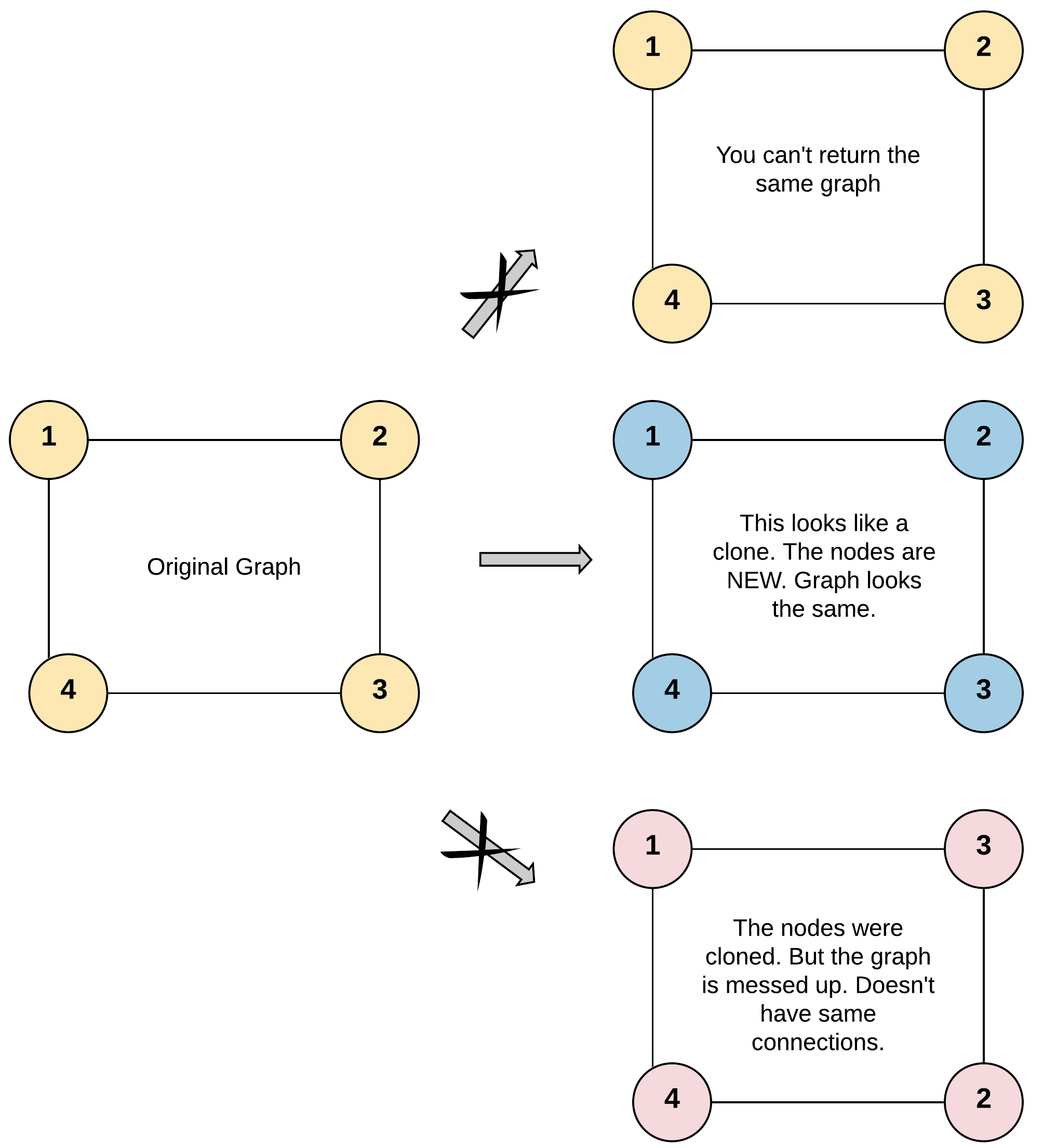
给你无向 连通 图中一个节点的引用,请你返回该图的 深拷贝(克隆)。
图中的每个节点都包含它的值 val(int) 和其邻居的列表(list[Node])。
class Node {
public int val;
public List<Node> neighbors;
}
测试用例格式:
简单起见,每个节点的值都和它的索引相同。例如,第一个节点值为 1(val = 1),第二个节点值为 2(val = 2),以此类推。该图在测试用例中使用邻接列表表示。
邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。
给定节点将始终是图中的第一个节点(值为 1)。你必须将 给定节点的拷贝 作为对克隆图的引用返回。
示例 1:
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。
示例 2:
输入:adjList = [[]]
输出:[[]]
解释:输入包含一个空列表。该图仅仅只有一个值为 1 的节点,它没有任何邻居。
示例 3:
输入:adjList = []
输出:[]
解释:这个图是空的,它不含任何节点。
提示:
- 这张图中的节点数在
[0, 100]之间。 1 <= Node.val <= 100- 每个节点值
Node.val都是唯一的, - 图中没有重复的边,也没有自环。
- 图是连通图,你可以从给定节点访问到所有节点。
思路
哈希表存现在图的各个节点和已复制的节点的对应关系
随后dfs图,如果遇到添加的节点还未new过,则new 一个节点存哈希表,如果已经存在了就直接取地址,不用哈希表的话就可能重复复制
代码
/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> neighbors;
Node() {
val = 0;
neighbors = vector<Node*>();
}
Node(int _val) {
val = _val;
neighbors = vector<Node*>();
}
Node(int _val, vector<Node*> _neighbors) {
val = _val;
neighbors = _neighbors;
}
};
*/
class Solution {
public:
Node* cloneGraph(Node* node) {
unordered_map<Node*,Node*> mirror;
function<Node*(Node*)> dfs = [&](Node* a)->Node*{
if(!a){
return nullptr;
}
if(mirror.count(a)){
return mirror[a];
}
Node* clone = new Node(a->val);
mirror[a] = clone;
for(int i=0;i<a->neighbors.size();i++){
if(!mirror.count(a->neighbors[i])){
Node* temp = dfs(a->neighbors[i]);
mirror[a]->neighbors.emplace_back(temp);
}else{
mirror[a]->neighbors.emplace_back(mirror[a->neighbors[i]]);
}
}
return mirror[a];
};
return dfs(node);
}
};
134. 加油站
题干
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
gas.length == ncost.length == n1 <= n <= 1050 <= gas[i], cost[i] <= 104
思路
枚举各个位置看其是否能走通环路,但是可以贪心法去跳过某些不必要的起始点,贪心的做法是每次跳过至当前轮次走过的最远路径节点
代码
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int n = gas.size();
int i = 0;
while (i < n) {
int sumOfGas = 0, sumOfCost = 0;
int cnt = 0;
while (cnt < n) {
int j = (i + cnt) % n;
sumOfGas += gas[j];
sumOfCost += cost[j];
if (sumOfCost > sumOfGas) {
break;
}
cnt++;
}
if (cnt == n) {
return i;
} else {
i = i + cnt + 1;
}
}
return -1;
}
};
137. 只出现一次的数字 II
题干
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
1 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1nums中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
思路
不允许用哈希表,就用位运算,由于数字最大为2^32位,枚举每个二进制数字位0-32,对于非答案的数字其在该数字位上出现0次或者3次被三整除,而对于只出现一次的数字来说其出现0次或者1次,因此如果该数字出现则该数字位出现1的次数必定是3k+1个,因此每个数字位计数后判断其是否不能被三整除将答案的该位置设为1 ,最后各个位置构成的二进制数就是答案
代码
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans = 0;
for (int i = 0; i < 32; ++i) {
int total = 0;
for (int num: nums) {
total += ((num >> i) & 1);
}
if (total % 3) {
ans |= (1 << i);
}
}
return ans;
}
};
138. 随机链表的复制
题干
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示Node.val的整数。random_index:随机指针指向的节点索引(范围从0到n-1);如果不指向任何节点,则为null。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:
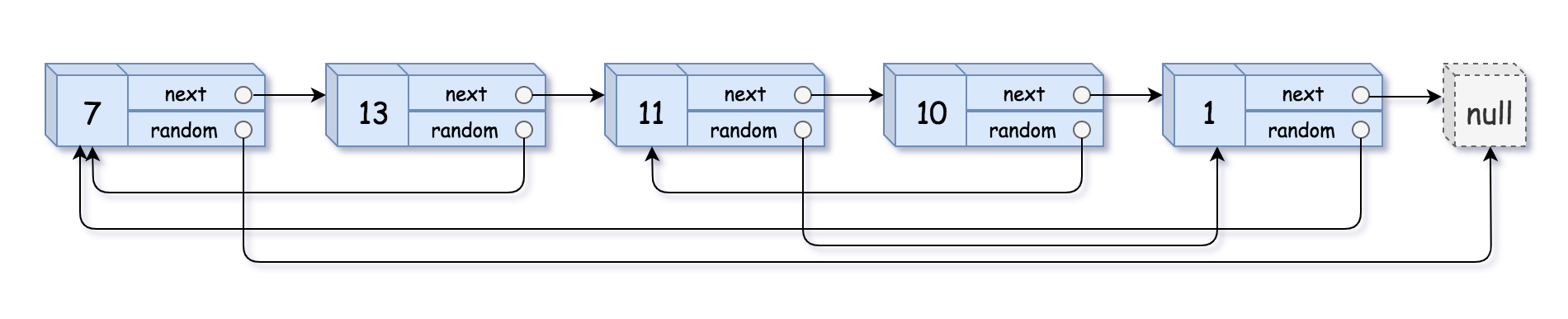
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:

输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:

输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
提示:
0 <= n <= 1000-104 <= Node.val <= 104Node.random为null或指向链表中的节点。
思路
凡是带有指针的数据结构的复制,就是用哈希表维护原node和复制node的对应关系,如果哈希表没有就new一个有就直接获取指针
代码
/*
// Definition for a Node.
class Node {
public:
int val;
Node* next;
Node* random;
Node(int _val) {
val = _val;
next = NULL;
random = NULL;
}
};
*/
class Solution {
public:
unordered_map<Node*,Node*> mp;
Node* copyRandomList(Node* head) {
if(!head){
return nullptr;
}
Node* temp = head;
Node* copyHead = new Node(head->val);
mp[head] = copyHead;
while(temp){
if(temp->next==nullptr){
mp[temp]->next = nullptr;
}else{
if(mp.count(temp->next)){
mp[temp]->next = mp[temp->next];
}else{
Node* copy = new Node(temp->next->val);
mp[temp->next] = copy;
mp[temp]->next = mp[temp->next];
}
}
if(temp->random==nullptr){
mp[temp]->random = nullptr;
}else{
if(mp.count(temp->random)){
mp[temp]->random = mp[temp->random];
}else{
Node* copy = new Node(temp->random->val);
mp[temp->random] = copy;
mp[temp]->random = mp[temp->random];
}
}
temp = temp->next;
}
return mp[head];
}
};
139. 单词拆分
题干
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
提示:
1 <= s.length <= 3001 <= wordDict.length <= 10001 <= wordDict[i].length <= 20s和wordDict[i]仅由小写英文字母组成wordDict中的所有字符串 互不相同
思路
记忆化搜索,即dfs的时候加缓存判断dfs的位置是否已经访问过,先将字典转化为哈希表,dfs(s,index)表示下一个单词从s[index]开始取,枚举单词结束的位置next,如果取到了单词,则dfs(s,next),如果next已经到了末尾说明找到答案
此外可以动态规划,dp[i]表示到i位置可以满足,每次遍历dp[0]到dp[i-1]看上一个true位置后到当前位置的substr是否在set里,只要有一个能满足则当前的dp[i]就是true
代码
class Solution {
public:
unordered_set<string> st;
unordered_map<int,int> visited;
bool answer;
void dfs(string s,int index){
if(answer==true){
return;
}
if(index==s.size()){
answer = true;
return;
}
int next = index+1;
for(int next=index+1;next<=s.size();next++){
if(visited.count(next)&&visited[next]>0){
continue;
}else if(st.count(s.substr(index,next-index))>0){
visited[next] = 1;
dfs(s,next);
}
}
};
bool wordBreak(string s, vector<string>& wordDict) {
answer = false;
for(auto x:wordDict){
st.insert(x);
}
dfs(s,0);
return answer;
}
};
142. 环形链表 II
题干
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
示例 1:

输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:

输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:

输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
- 链表中节点的数目范围在范围
[0, 104]内 -105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引
进阶:你是否可以使用 O(1) 空间解决此题?
思路
快慢指针加上数学的分析(也可以找规律),找到重合位置Node a,再令temp1 = a,temp2=head,让这两个指针同步向前,它们的再次重合的位置Node b即为答案
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head;
ListNode *slow = head;
bool hascycle = false;
while(fast){
fast = fast->next;
slow = slow->next;
if(!fast||!fast->next){
break;
}
fast = fast->next;
if(fast==slow){
hascycle = true;
break;
}
}
if(!hascycle){return nullptr;}
else{
ListNode *temp=head;
while(temp!=slow){
temp = temp->next;
slow = slow->next;
}
return slow;
}
}
};
143. 重排链表
题干
给定一个单链表 L 的头节点 head ,单链表 L 表示为:
L0 → L1 → … → Ln - 1 → Ln
请将其重新排列后变为:
L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
不能只是单纯的改变节点内部的值,而是需要实际的进行节点交换。
示例 1:
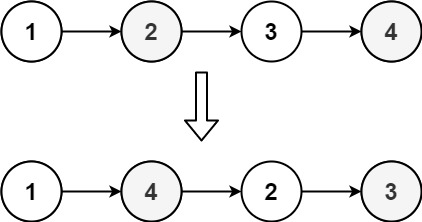
输入:head = [1,2,3,4]
输出:[1,4,2,3]
示例 2:
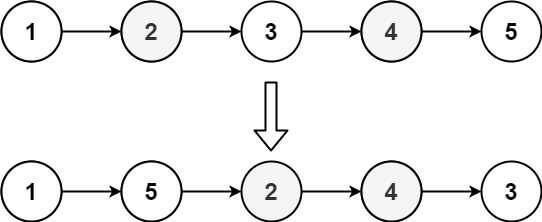
输入:head = [1,2,3,4,5]
输出:[1,5,2,4,3]
提示:
- 链表的长度范围为
[1, 5 * 104] 1 <= node.val <= 1000
思路
链表的大部分问题无非是用到合并两个链表、翻转链表、快慢指针找链表中点,本题就是先找到链表中点,断开成两个链表A,B,将链表B翻转为B‘,最后按照顺序合并A和B’
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverselist(ListNode* head){
ListNode* pre = nullptr;
ListNode* now = head;
while(now){
ListNode* nxt = now->next;
now->next = pre;
pre = now;
now = nxt;
}
return pre;
}
void reorderList(ListNode* head) {
if(!head||!head->next){
return ;
}
ListNode* dummy = new ListNode();
dummy->next = head;
int length = 0;
ListNode* help = head;
while(help){
length++;
help = help->next;
}
int mid;
if(length%2==0){
mid = length/2;
}else{
mid = length/2+1;
}
help = dummy;
for(int i=0;i<mid;i++){
help = help->next;
}
ListNode* order2 = help->next;
help->next = nullptr;
order2 = reverselist(order2);
ListNode* order1 = dummy->next;
ListNode* dummy2 = new ListNode();
help = dummy2;
int flag = 1;
while(order1||order2){
if(flag==1){
flag = -flag;
help->next = order1;
help = help->next;
if(order1){
order1 = order1->next;
}
}else{
flag = -flag;
help->next = order2;
help = help->next;
if(order2){
order2 = order2->next;
}
}
}
}
};
146. LRU 缓存
题干
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以 正整数 作为容量capacity初始化 LRU 缓存int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回-1。void put(int key, int value)如果关键字key已经存在,则变更其数据值value;如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 30000 <= key <= 100000 <= value <= 105- 最多调用
2 * 105次get和put
思路
用到了哈希表和双向链表,哈希表记录key的节点,使用双向链表是为了删除节点方便,lru的思想是如果get或者put了说明使用了,将当前节点删除,添加到双向链表的头部,如果是put则判断是否超过cache size,超过则删除尾部节点
代码
struct DLinkedNode {
int key, value;
DLinkedNode* prev;
DLinkedNode* next;
DLinkedNode(): key(0), value(0), prev(nullptr), next(nullptr) {}
DLinkedNode(int _key, int _value): key(_key), value(_value), prev(nullptr), next(nullptr) {}
};
class LRUCache {
private:
unordered_map<int, DLinkedNode*> cache;
DLinkedNode* head;
DLinkedNode* tail;
int size;
int capacity;
public:
LRUCache(int _capacity): capacity(_capacity), size(0) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head->next = tail;
tail->prev = head;
}
int get(int key) {
if (!cache.count(key)) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
DLinkedNode* node = cache[key];
moveToHead(node);
return node->value;
}
void put(int key, int value) {
if (!cache.count(key)) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode* node = new DLinkedNode(key, value);
// 添加进哈希表
cache[key] = node;
// 添加至双向链表的头部
addToHead(node);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode* removed = removeTail();
// 删除哈希表中对应的项
cache.erase(removed->key);
// 防止内存泄漏
delete removed;
--size;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
DLinkedNode* node = cache[key];
node->value = value;
moveToHead(node);
}
}
void addToHead(DLinkedNode* node) {
node->prev = head;
node->next = head->next;
head->next->prev = node;
head->next = node;
}
void removeNode(DLinkedNode* node) {
node->prev->next = node->next;
node->next->prev = node->prev;
}
void moveToHead(DLinkedNode* node) {
removeNode(node);
addToHead(node);
}
DLinkedNode* removeTail() {
DLinkedNode* node = tail->prev;
removeNode(node);
return node;
}
};
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/
147. 对链表进行插入排序
题干
给定单个链表的头 head ,使用 插入排序 对链表进行排序,并返回 排序后链表的头 。
插入排序 算法的步骤:
- 插入排序是迭代的,每次只移动一个元素,直到所有元素可以形成一个有序的输出列表。
- 每次迭代中,插入排序只从输入数据中移除一个待排序的元素,找到它在序列中适当的位置,并将其插入。
- 重复直到所有输入数据插入完为止。
下面是插入排序算法的一个图形示例。部分排序的列表(黑色)最初只包含列表中的第一个元素。每次迭代时,从输入数据中删除一个元素(红色),并就地插入已排序的列表中。
对链表进行插入排序。

示例 1:
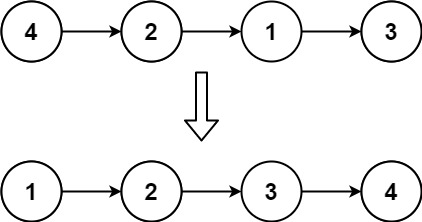
输入: head = [4,2,1,3]
输出: [1,2,3,4]
示例 2:
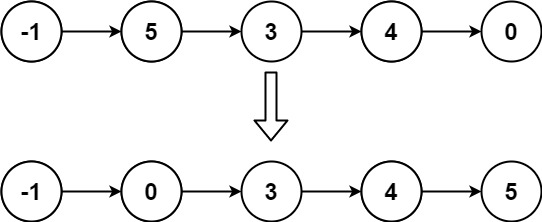
输入: head = [-1,5,3,4,0]
输出: [-1,0,3,4,5]
提示:
- 列表中的节点数在
[1, 5000]范围内 -5000 <= Node.val <= 5000
思路
遍历链表然后插入排序,注意dummy节点的使用,最后返回dummy节点的next
代码
class Solution {
public:
ListNode *insert(ListNode *head, ListNode *node) {//将节点node插入head为头的有序链表, 返回插入后的有序链表头部
ListNode *h0 = new ListNode(-1, head);
ListNode *cur = h0;
while (cur->next && node->val > cur->next->val)
cur = cur->next;
node->next = cur->next;
cur->next = node;
return h0->next;
}
ListNode *insertionSortList(ListNode *head) {
ListNode *h = nullptr;
for (ListNode *cur = head, *next; cur; cur = next) {//遍历链表中的节点
next = cur->next;
h = insert(h, cur);
}
return h;
}
};
148. 排序链表
题干
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:

输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:

输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
提示:
- 链表中节点的数目在范围
[0, 5 * 104]内 -105 <= Node.val <= 105
进阶:你可以在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
思路
可以使用之前做过的插入排序,但是效率低,更好的是使用链表的归并排序,这里用到了快慢指针找到链表的中点以及合并两个有序链表的代码,自上而下归并即可
代码
class Solution {
public:
ListNode* sortList(ListNode* head) {
return sortList(head, nullptr);
}
ListNode* sortList(ListNode* head, ListNode* tail) {
if (head == nullptr) {
return head;
}
if (head->next == tail) {
head->next = nullptr;
return head;
}
ListNode* slow = head, *fast = head;
while (fast != tail) {
slow = slow->next;
fast = fast->next;
if (fast != tail) {
fast = fast->next;
}
}
ListNode* mid = slow;
return merge(sortList(head, mid), sortList(mid, tail));
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
};
150. 逆波兰表达式求值
题干
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*'和'/'。 - 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
提示:
1 <= tokens.length <= 104tokens[i]是一个算符("+"、"-"、"*"或"/"),或是在范围[-200, 200]内的一个整数
逆波兰表达式:
逆波兰表达式是一种后缀表达式,所谓后缀就是指算符写在后面。
- 平常使用的算式则是一种中缀表达式,如
( 1 + 2 ) * ( 3 + 4 )。 - 该算式的逆波兰表达式写法为
( ( 1 2 + ) ( 3 4 + ) * )。
逆波兰表达式主要有以下两个优点:
- 去掉括号后表达式无歧义,上式即便写成
1 2 + 3 4 + *也可以依据次序计算出正确结果。 - 适合用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
思路
用栈操作运算:遇到数字则入栈;遇到算符则取出栈顶两个数字进行计算,并将结果压入栈中
代码
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> stk;
int n = tokens.size();
for (int i = 0; i < n; i++) {
string& token = tokens[i];
if (isNumber(token)) {
stk.push(atoi(token.c_str()));
} else {
int num2 = stk.top();
stk.pop();
int num1 = stk.top();
stk.pop();
switch (token[0]) {
case '+':
stk.push(num1 + num2);
break;
case '-':
stk.push(num1 - num2);
break;
case '*':
stk.push(num1 * num2);
break;
case '/':
stk.push(num1 / num2);
break;
}
}
}
return stk.top();
}
bool isNumber(string& token) {
return !(token == "+" || token == "-" || token == "*" || token == "/");
}
};
151. 反转字符串中的单词
题干
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue"
输出:"blue is sky the"
示例 2:
输入:s = " hello world "
输出:"world hello"
解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
输入:s = "a good example"
输出:"example good a"
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
提示:
1 <= s.length <= 104s包含英文大小写字母、数字和空格' 's中 至少存在一个 单词
进阶:如果字符串在你使用的编程语言中是一种可变数据类型,请尝试使用 O(1) 额外空间复杂度的 原地 解法。
思路
c++关于split或者类型转换时先想到stringstream,不能满足时再自己写split函数,本题split后重新倒序拼接单词即可
代码
class Solution {
public:
string reverseWords(string s) {
vector<string> v;
stringstream ss(s);
string temp;
while(ss>>temp){
v.emplace_back(temp);
}
string answer;
for(int i=v.size()-1;i>=0;i--){
answer += v[i];
if(i!=0){
answer+=" ";
}
}
return answer;
}
};
152. 乘积最大子数组
题干
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续
子数组
(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 104-10 <= nums[i] <= 10nums的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
思路
两个数组的动态规划(其实就是二维),一个维度记录历史乘积最小值,一个记录最大值,这是因为当前数字可能是正可能是负,正的找上一个正的最大,负的找上一个负的最小
代码
class Solution {
public:
int maxProduct(vector<int>& nums) {
vector<int> maxF(nums.size());
vector<int> minF(nums.size());
maxF[0] = nums[0];
minF[0] = nums[0];
int answer = nums[0];
for(int i=1;i<nums.size();i++){
maxF[i] = max(maxF[i - 1] * nums[i], max(nums[i], minF[i - 1] * nums[i]));
if(maxF[i]>answer){
answer = maxF[i];
}
minF[i] = min(minF[i - 1] * nums[i], min(nums[i], maxF[i - 1] * nums[i]));
}
return answer;
}
};
153. 寻找旋转排序数组中的最小值
题干
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
n == nums.length1 <= n <= 5000-5000 <= nums[i] <= 5000nums中的所有整数 互不相同nums原来是一个升序排序的数组,并进行了1至n次旋转
思路
二分法,根据mid和right的比较判断最小值接下来在哪个区域
代码
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0;
int right = nums.size()-1;
while(left<right){
int mid = left+(right-left)/2;
if(nums[mid]>nums[right]){
left = mid+1;
}else{
right = mid;
}
}
return nums[right];
}
};
155. 最小栈
题干
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack()初始化堆栈对象。void push(int val)将元素val推入堆栈。void pop()删除堆栈顶部的元素。int top()获取堆栈顶部的元素。int getMin()获取堆栈中的最小元素。
示例 1:
输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
提示:
-231 <= val <= 231 - 1pop、top和getMin操作总是在 非空栈 上调用push,pop,top, andgetMin最多被调用3 * 104次
思路
用两个栈,一个栈就是普通的栈,另一个是用来同步当前最小值的同步栈,push和pop都同步操作
代码
class MinStack {
public:
vector<int> stack;
vector<int> minStack;
MinStack() {
}
void push(int val) {
if(stack.size()==0){
minStack.emplace_back(val);
}else{
minStack.emplace_back(min(val,minStack.back()));
}
stack.emplace_back(val);
}
void pop() {
stack.pop_back();
minStack.pop_back();
}
int top() {
return stack.back();
}
int getMin() {
return minStack.back();
}
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/
156. 上下翻转二叉树
题干
给你一个二叉树的根节点 root ,请你将此二叉树上下翻转,并返回新的根节点。
你可以按下面的步骤翻转一棵二叉树:
- 原来的左子节点变成新的根节点
- 原来的根节点变成新的右子节点
- 原来的右子节点变成新的左子节点

上面的步骤逐层进行。题目数据保证每个右节点都有一个同级节点(即共享同一父节点的左节点)且不存在子节点。
示例 1:
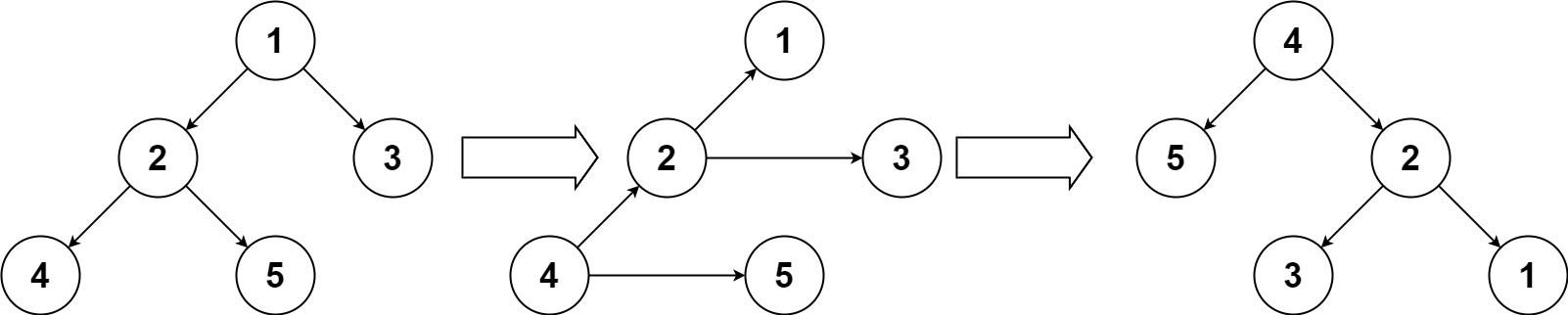
输入:root = [1,2,3,4,5]
输出:[4,5,2,null,null,3,1]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
提示:
- 树中节点数目在范围
[0, 10]内 1 <= Node.val <= 10- 树中的每个右节点都有一个同级节点(即共享同一父节点的左节点)
- 树中的每个右节点都没有子节点
思路
dfs递归,每次传入father,l,r三个节点,下次递归是l,l.left,l.right,其中l.left,l.right每次要单独存下来(因为l的left要连到上次递归的节点上)
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* upsideDownBinaryTree(TreeNode* root) {
if(!root||!root->left){
return root;
}
function<TreeNode*(TreeNode*,TreeNode*,TreeNode*)> dfs = [&](TreeNode* father,TreeNode* l,TreeNode* r){
if(!l){
return father;
}
TreeNode* nextLeft = l->left;
TreeNode* nextRight = l->right;
l->left = r;
l->right = father;
return dfs(l,nextLeft,nextRight);
};
return dfs(nullptr,root,nullptr);
}
};
159. 至多包含两个不同字符的最长子串
题干
给你一个字符串 s ,请你找出 至多 包含 两个不同字符 的最长子串,并返回该子串的长度。
示例 1:
输入:s = "eceba"
输出:3
解释:满足题目要求的子串是 "ece" ,长度为 3 。
示例 2:
输入:s = "ccaabbb"
输出:5
解释:满足题目要求的子串是 "aabbb" ,长度为 5 。
提示:
1 <= s.length <= 105s由英文字母组成
思路
滑动窗口加哈希表,求出所有满足题意的子数组,求最长那个
代码
class Solution {
public:
int lengthOfLongestSubstringTwoDistinct(string s) {
unordered_map<char,int> mp;
int diff_num = 0;
int answer = 0;
int l = 0;
for(int r=0;r<s.size();r++){
mp[s[r]]+=1;
if(mp.size()<=2){
answer = max(answer,r-l+1);
}else{
while(mp.size()>2){
mp[s[l]]--;
if(mp[s[l]]==0){
mp.erase(s[l]);
}
l++;
}
answer = max(answer,r-l+1);
}
}
return answer;
}
};
161. 相隔为 1 的编辑距离
题干
给定两个字符串 s 和 t ,如果它们的编辑距离为 1 ,则返回 true ,否则返回 false 。
字符串 s 和字符串 t 之间满足编辑距离等于 1 有三种可能的情形:
- 往
s中插入 恰好一个 字符得到t - 从
s中删除 恰好一个 字符得到t - 在
s中用 一个不同的字符 替换 恰好一个 字符得到t
示例 1:
输入: s = "ab", t = "acb"
输出: true
解释: 可以将 'c' 插入字符串 s 来得到 t。
示例 2:
输入: s = "cab", t = "ad"
输出: false
解释: 无法通过 1 步操作使 s 变为 t。
提示:
0 <= s.length, t.length <= 104s和t由小写字母,大写字母和数字组成
思路
按照编辑距离72. 编辑距离做二维dp,判断右下角答案是否为1
代码
class Solution {
public:
bool isOneEditDistance(string s, string t) {
vector<vector<int>> distance(s.size()+1,vector<int>(t.size()+1));
int temp = 0;
for(int i=0;i<distance.size();i++){
distance[i][0] = temp;
temp++;
}
temp = 0;
for(int j=0;j<distance[0].size();j++){
distance[0][j] = temp;
temp++;
}
for(int i=1;i<distance.size();i++){
for(int j=1;j<distance[0].size();j++){
if(s[i-1]==t[j-1]){
distance[i][j] = min(distance[i-1][j-1],min(distance[i-1][j]+1,distance[i][j-1]+1));
}else{
distance[i][j] = min(distance[i-1][j-1]+1,min(distance[i-1][j]+1,distance[i][j-1]+1));
}
}
}
return distance[s.size()][t.size()]==1;
}
};
162. 寻找峰值
题干
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
提示:
1 <= nums.length <= 1000-231 <= nums[i] <= 231 - 1- 对于所有有效的
i都有nums[i] != nums[i + 1]
思路
二分查找,爬坡法,判断mid在上坡还是下坡,从而判断在那个半边继续二分
代码
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right) {
int mid = (left + right) >> 1;
if (nums[mid] > nums[mid + 1]) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
};
164. 最大间距
题干
给定一个无序的数组 nums,返回 数组在排序之后,相邻元素之间最大的差值 。如果数组元素个数小于 2,则返回 0 。
您必须编写一个在「线性时间」内运行并使用「线性额外空间」的算法。
示例 1:
输入: nums = [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。
示例 2:
输入: nums = [10]
输出: 0
解释: 数组元素个数小于 2,因此返回 0。
提示:
1 <= nums.length <= 1050 <= nums[i] <= 109
思路
基数排序(桶排序)后复杂度O(nk),k为排序的轮数(数组中最大值的位数),随后寻找相邻的最大值即可
代码
class Solution {
public:
int maximumGap(vector<int>& nums) {
int n = nums.size();
//如果数组元素个数小于 2,则返回 0
if(n < 2)
{
return 0;
}
vector<int> buf(n); //buf为临时顺组,用于存储每次排完序的数组
int maxVal = *max_element(nums.begin(), nums.end());
int time = maxBit(maxVal); //计算出需要最高位数,即需要排多少次
int dev = 1;
//开始从低位到高位基数排序
for(int i = 0; i < time; i++){
vector<vector<int>> count(10); //桶
//统计每个桶中有多少个数
for(int j = 0; j < n; j++){
int digit = (nums[j] / dev) % 10; //digit 为nums[j]的第i位数
count[digit].emplace_back(nums[j]);
}
int index = n-1;
for(int number = 9;number>=0;number--){
while(count[number].size()>0){
nums[index] = count[number].back();
count[number].pop_back();
index--;
}
}
dev *= 10;
}
//找到相邻元素最大差值
int ret = 0;
for (int i = 1; i < n; i++) {
ret = max(ret, nums[i] - nums[i - 1]);
}
return ret;
}
int maxBit(int maxVal){
int p = 10;
int d = 1;
while(maxVal >= p){
p *= 10;
d++;
}
return d;
}
};
165. 比较版本号
题干
给你两个版本号 version1 和 version2 ,请你比较它们。
版本号由一个或多个修订号组成,各修订号由一个 '.' 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。
比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。
返回规则如下:
- 如果
*version1* > *version2*返回1, - 如果
*version1* < *version2*返回-1, - 除此之外返回
0。
示例 1:
输入:version1 = "1.01", version2 = "1.001"
输出:0
解释:忽略前导零,"01" 和 "001" 都表示相同的整数 "1"
示例 2:
输入:version1 = "1.0", version2 = "1.0.0"
输出:0
解释:version1 没有指定下标为 2 的修订号,即视为 "0"
示例 3:
输入:version1 = "0.1", version2 = "1.1"
输出:-1
解释:version1 中下标为 0 的修订号是 "0",version2 中下标为 0 的修订号是 "1" 。0 < 1,所以 version1 < version2
提示:
1 <= version1.length, version2.length <= 500version1和version2仅包含数字和'.'version1和version2都是 有效版本号version1和version2的所有修订号都可以存储在 32 位整数 中
思路
把版本号按照‘.’分割(自己写分割或者使用stringstream),分别将每段转int后存入两个vector中,对于短的vector在后面补充0至齐平,最后从位置0开始比较两个vector的对应位置大小
代码
class Solution {
public:
int compareVersion(string version1, string version2) {
vector<int> v1;
vector<int> v2;
int start = 0;
int end = 0;
while(end!=version1.size()){
end++;
if(version1[end]=='.'){
string temp = version1.substr(start,end-start);
v1.emplace_back(atoi(temp.c_str()));
start = end+1;
end = start;
}
}
if(end>start){
string temp = version1.substr(start,end-start);
v1.emplace_back(atoi(temp.c_str()));
}
start = 0;
end = 0;
while(end!=version2.size()){
end++;
if(version2[end]=='.'){
string temp = version2.substr(start,end-start);
v2.emplace_back(atoi(temp.c_str()));
start = end+1;
end = start;
}
}
if(end>start){
string temp = version2.substr(start,end-start);
v2.emplace_back(atoi(temp.c_str()));
}
while(v1.size()<v2.size()){
v1.emplace_back(0);
}
while(v2.size()<v1.size()){
v2.emplace_back(0);
}
for(int i=0;i<v1.size();i++){
if(v1[i]>v2[i]){
return 1;
}
if(v1[i]<v2[i]){
return -1;
}
}
return 0;
}
};
166. 分数到小数
题干
思路
代码
class Solution {
public:
string fractionToDecimal(int numerator, int denominator) {
long numeratorLong = numerator;
long denominatorLong = denominator;
if (numeratorLong % denominatorLong == 0) {
return to_string(numeratorLong / denominatorLong);
}
string ans;
if (numeratorLong < 0 ^ denominatorLong < 0) {
ans.push_back('-');
}
// 整数部分
numeratorLong = abs(numeratorLong);
denominatorLong = abs(denominatorLong);
long integerPart = numeratorLong / denominatorLong;
ans += to_string(integerPart);
ans.push_back('.');
// 小数部分
string fractionPart;
unordered_map<long, int> remainderIndexMap;
long remainder = numeratorLong % denominatorLong;
int index = 0;
while (remainder != 0 && !remainderIndexMap.count(remainder)) {
remainderIndexMap[remainder] = index;
remainder *= 10;
fractionPart += to_string(remainder / denominatorLong);
remainder %= denominatorLong;
index++;
}
if (remainder != 0) { // 有循环节
int insertIndex = remainderIndexMap[remainder];
fractionPart = fractionPart.substr(0,insertIndex) + '(' + fractionPart.substr(insertIndex);
fractionPart.push_back(')');
}
ans += fractionPart;
return ans;
}
};
166. 分数到小数
题干
给定两个整数,分别表示分数的分子 numerator 和分母 denominator,以 字符串形式返回小数 。
如果小数部分为循环小数,则将循环的部分括在括号内。
如果存在多个答案,只需返回 任意一个 。
对于所有给定的输入,保证 答案字符串的长度小于 104 。
示例 1:
输入:numerator = 1, denominator = 2
输出:"0.5"
示例 2:
输入:numerator = 2, denominator = 1
输出:"2"
示例 3:
输入:numerator = 4, denominator = 333
输出:"0.(012)"
提示:
-231 <= numerator, denominator <= 231 - 1denominator != 0
思路
模拟长除法,整数部分直接除法取整即可,小数部分哈希表记录remainder(当前被除数)和对应index,如果发现重复了说明是循环小数就退出长除
代码
class Solution {
public:
string fractionToDecimal(int numerator, int denominator) {
long numeratorLong = numerator;
long denominatorLong = denominator;
if (numeratorLong % denominatorLong == 0) {
return to_string(numeratorLong / denominatorLong);
}
string ans;
if (numeratorLong < 0 ^ denominatorLong < 0) {
ans.push_back('-');
}
// 整数部分
numeratorLong = abs(numeratorLong);
denominatorLong = abs(denominatorLong);
long integerPart = numeratorLong / denominatorLong;
ans += to_string(integerPart);
ans.push_back('.');
// 小数部分
string fractionPart;
unordered_map<long, int> remainderIndexMap;
long remainder = numeratorLong % denominatorLong;
int index = 0;
while (remainder != 0 && !remainderIndexMap.count(remainder)) {
remainderIndexMap[remainder] = index;
remainder *= 10;
fractionPart += to_string(remainder / denominatorLong);
remainder %= denominatorLong;
index++;
}
if (remainder != 0) { // 有循环节
int insertIndex = remainderIndexMap[remainder];
fractionPart = fractionPart.substr(0,insertIndex) + '(' + fractionPart.substr(insertIndex);
fractionPart.push_back(')');
}
ans += fractionPart;
return ans;
}
};
167. 两数之和 II - 输入有序数组
题干
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示:
2 <= numbers.length <= 3 * 104-1000 <= numbers[i] <= 1000numbers按 非递减顺序 排列-1000 <= target <= 1000- 仅存在一个有效答案
思路
可以用1. 两数之和去做,但是本题已经有序的话可以按顺序固定一个数,再在这个数之后的数组中二分查找另一个数,找到说明有答案
代码
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
for (int i = 0; i < numbers.size(); ++i) {
int low = i + 1, high = numbers.size() - 1;
while (low <= high) {
int mid = (high - low) / 2 + low;
if (numbers[mid] == target - numbers[i]) {
return {i + 1, mid + 1};
} else if (numbers[mid] > target - numbers[i]) {
high = mid - 1;
} else {
low = mid + 1;
}
}
}
return {-1, -1};
}
};
172. 阶乘后的零
题干
给定一个整数 n ,返回 n! 结果中尾随零的数量。
提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1
示例 1:
输入:n = 3
输出:0
解释:3! = 6 ,不含尾随 0
示例 2:
输入:n = 5
输出:1
解释:5! = 120 ,有一个尾随 0
示例 3:
输入:n = 0
输出:0
提示:
0 <= n <= 104
进阶:你可以设计并实现对数时间复杂度的算法来解决此问题吗?
思路
小学奥数题,由于10=5*2,对于阶乘来说5的数量远远大于2的数量,因此本题转化为各个数字中存在多少5,累加即可
代码
class Solution {
public:
int trailingZeroes(int n) {
int ans = 0;
for (int i = 5; i <= n; i += 5) {
for (int x = i; x % 5 == 0; x /= 5) {
++ans;
}
}
return ans;
}
};
173. 二叉搜索树迭代器
题干
实现一个二叉搜索树迭代器类BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点root会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。boolean hasNext()如果向指针右侧遍历存在数字,则返回true;否则返回false。int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
示例:

输入
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
输出
[null, 3, 7, true, 9, true, 15, true, 20, false]
解释
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next(); // 返回 3
bSTIterator.next(); // 返回 7
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 9
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 15
bSTIterator.hasNext(); // 返回 True
bSTIterator.next(); // 返回 20
bSTIterator.hasNext(); // 返回 False
提示:
- 树中节点的数目在范围
[1, 105]内 0 <= Node.val <= 106- 最多调用
105次hasNext和next操作
进阶:
- 你可以设计一个满足下述条件的解决方案吗?
next()和hasNext()操作均摊时间复杂度为O(1),并使用O(h)内存。其中h是树的高度。
思路
用栈模拟中序dfs,维护当前访问的Treenode即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class BSTIterator {
private:
TreeNode* cur;
stack<TreeNode*> stk;
public:
BSTIterator(TreeNode* root): cur(root) {}
int next() {
while (cur != nullptr) {
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
stk.pop();
int ret = cur->val;
cur = cur->right;
return ret;
}
bool hasNext() {
return cur != nullptr || !stk.empty();
}
};
/**
* Your BSTIterator object will be instantiated and called as such:
* BSTIterator* obj = new BSTIterator(root);
* int param_1 = obj->next();
* bool param_2 = obj->hasNext();
*/
179. 最大数
题干
给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。
注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。
示例 1:
输入:nums = [10,2]
输出:"210"
示例 2:
输入:nums = [3,30,34,5,9]
输出:"9534330"
提示:
1 <= nums.length <= 1000 <= nums[i] <= 109
思路
转化成vector<string>后自定义排序并拼接,这里的string a和string b的排序规则是a+b>b+a
代码
class Solution {
public:
string largestNumber(vector<int>& nums) {
vector<string> strs;
for(int i=0;i<nums.size();i++){
strs.emplace_back(to_string(nums[i]));
}
sort(strs.begin(),strs.end(),[&](const string &a,const string &b){
return a+b>b+a;
});
int notzero = 0;
string answer="";
for(auto &x:strs){
answer+=x;
}
string answer2="";
int zero = 0;
for(int i=0;i<answer.size();i++){
if(zero==0&&answer[i]=='0'){
continue;
}else{
zero = 1;
answer2+=answer[i];
}
}
return answer2.size()==0?"0":answer2;
}
};
186. 反转字符串中的单词 II
题干
给你一个字符数组 s ,反转其中 单词 的顺序。
单词 的定义为:单词是一个由非空格字符组成的序列。s 中的单词将会由单个空格分隔。
必须设计并实现 原地 解法来解决此问题,即不分配额外的空间。
示例 1:
输入:s = ["t","h","e"," ","s","k","y"," ","i","s"," ","b","l","u","e"]
输出:["b","l","u","e"," ","i","s"," ","s","k","y"," ","t","h","e"]
示例 2:
输入:s = ["a"]
输出:["a"]
提示:
1 <= s.length <= 105s[i]可以是一个英文字母(大写或小写)、数字、或是空格' '。s中至少存在一个单词s不含前导或尾随空格- 题目数据保证:
s中的每个单词都由单个空格分隔
思路
先整体翻转,再双指针确定每个单词的left和right,对于[left,right]范围内的字符进行reverse
代码
class Solution {
public:
void reverseOneWord(vector<char>& s,int left,int right){
while(left<right){
int temp = s[left];
s[left] = s[right];
s[right] = temp;
left++;
right--;
}
}
void reverseWords(vector<char>& s) {
reverse(s.begin(),s.end());
int start = 0;
int end = 0;
int n = s.size();
while(end+1<n){
if(s[end+1]==' '){
reverseOneWord(s, start, end);
start = end+2;
end = start;
}else{
end++;
}
}
reverseOneWord(s, start, end); //最后一个单词
}
};
187. 重复的DNA序列
题干
DNA序列 由一系列核苷酸组成,缩写为 'A', 'C', 'G' 和 'T'.。
- 例如,
"ACGAATTCCG"是一个 DNA序列 。
在研究 DNA 时,识别 DNA 中的重复序列非常有用。
给定一个表示 DNA序列 的字符串 s ,返回所有在 DNA 分子中出现不止一次的 长度为 10 的序列(子字符串)。你可以按 任意顺序 返回答案。
示例 1:
输入:s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
输出:["AAAAACCCCC","CCCCCAAAAA"]
示例 2:
输入:s = "AAAAAAAAAAAAA"
输出:["AAAAAAAAAA"]
提示:
0 <= s.length <= 105s[i]``==``'A'、'C'、'G'or'T'
思路
滑动窗口加哈希表,这里的优化技巧是将字母映射为数字然后用位运算保存int值,如果该int值出现过两次则将序列加入答案
代码
class Solution {
const int L = 10;
unordered_map<char, int> bin = {{'A', 0}, {'C', 1}, {'G', 2}, {'T', 3}};
public:
vector<string> findRepeatedDnaSequences(string s) {
vector<string> ans;
int n = s.length();
if (n <= L) {
return ans;
}
int x = 0;
for (int i = 0; i < L-1 ; ++i) {
x = (x << 2) | bin[s[i]];
}
unordered_map<int, int> cnt;
for (int i = 0; i <= n - L; ++i) {
x = ((x << 2) | bin[s[i + L - 1]]) & ((1 << (L * 2)) - 1);
if (++cnt[x] == 2) {
ans.push_back(s.substr(i, L));
}
}
return ans;
}
};
189. 轮转数组
题干
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105-231 <= nums[i] <= 231 - 10 <= k <= 105
进阶:
- 尽可能想出更多的解决方案,至少有 三种 不同的方法可以解决这个问题。
- 你可以使用空间复杂度为
O(1)的 原地 算法解决这个问题吗?
思路
将轮转转化为三次翻转,可以举个例子翻转试试看
代码
class Solution {
public:
void reverse(vector<int>& nums, int start, int end) {
while (start < end) {
swap(nums[start], nums[end]);
start += 1;
end -= 1;
}
}
void rotate(vector<int>& nums, int k) {
k %= nums.size();
reverse(nums, 0, nums.size() - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.size() - 1);
}
};
198. 打家劫舍
题干
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
思路
一维动态规划,dp[i]表示到i位置结尾时的最大值,dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
代码
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.size()==0) {
return 0;
}
int size = nums.size();
if (size == 1) {
return nums[0];
}
vector<int> dp = vector<int>(size, 0);
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for (int i = 2; i < size; i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[size - 1];
}
};
199. 二叉树的右视图
题干
给定一个二叉树的 根节点
root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。示例 1:
![img]()
输入: [1,2,3,null,5,null,4] 输出: [1,3,4]示例 2:
输入: [1,null,3] 输出: [1,3]示例 3:
输入: [] 输出: []提示:
- 二叉树的节点个数的范围是
[0,100] -100 <= Node.val <= 100
- 二叉树的节点个数的范围是
思路
bfs树,每次记录每一层的最后一个值即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
queue<TreeNode*> q;
vector<int> answer;
if(!root) return {};
q.push(root);
while(q.size()>0){
int len = q.size();
for(int i=0;i<len;i++){
TreeNode* temp = q.front();
q.pop();
if(temp->left){
q.push(temp->left);
}
if(temp->right){
q.push(temp->right);
}
if(i==len-1){
answer.push_back(temp->val);
}
}
}
return answer;
}
};
200. 岛屿数量
题干
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 300grid[i][j]的值为'0'或'1'
思路
对每个点进行dfs,建立visited数组,每次dfs会将一个岛屿的所有点都设置为visited=1,因此只要visited=0且grid[i][j]=1说明有一个新岛屿
代码
class Solution {
public:
int dx[4]={0,-1,0,1};
int dy[4]={1,0,-1,0};
int answer = 0;
vector<vector<int>> isReached;
void dfs(vector<vector<char>>& grid, int x, int y) {
if(grid[x][y]=='1'&&isReached[x][y]==0){
isReached[x][y] = 1;
int xLength=grid.size();
int yLength=grid[0].size();
for(int i=0;i<4;i++){
if(x+dx[i]>=0&&x+dx[i]<xLength&&y+dy[i]>=0&&y+dy[i]<yLength)
{
dfs(grid,x+dx[i],y+dy[i]);
}
}
}
}
int numIslands(vector<vector<char>>& grid) {
int xLength=grid.size();
int yLength=grid[0].size();
isReached = vector<vector<int>>(xLength, vector<int>(yLength));
for(int i=0;i<grid.size();i++){
for(int j=0;j<grid[0].size();j++){
if(grid[i][j]=='1'&&isReached[i][j]==0){
answer++;
dfs(grid,i,j);
}
}
}
return answer;
}
};

