201. 数字范围按位与
题干
给你两个整数 left 和 right ,表示区间 [left, right] ,返回此区间内所有数字 按位与 的结果(包含 left 、right 端点)。
示例 1:
输入:left = 5, right = 7
输出:4
示例 2:
输入:left = 0, right = 0
输出:0
示例 3:
输入:left = 1, right = 2147483647
输出:0
提示:
0 <= left <= right <= 231 - 1
思路
数学位运算小技巧,直接遍历取与会超时,实际上连续数组取与只与第一个数和最后一个数有关,且答案是两个数的公共前缀,其余部分补零
代码
class Solution {
public:
int rangeBitwiseAnd(int m, int n) {
int shift = 0;
// 找到公共前缀
while (m < n) {
m >>= 1;
n >>= 1;
++shift;
}
return m << shift;
}
};
204. 计数质数
题干
给定整数 n ,返回 所有小于非负整数 n 的质数的数量 。
示例 1:
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
示例 2:
输入:n = 0
输出:0
示例 3:
输入:n = 1
输出:0
提示:
0 <= n <= 5 * 106
思路
素筛法,建立一个dp数组,初始值为1,从左往右取值,将其的倍数的dp值都置为0,最后dp里为1的就是质数
代码
class Solution {
public:
int countPrimes(int n) {
vector<int> isPrime(n, 1);
int ans = 0;
for (int i = 2; i < n; ++i) {
if (isPrime[i]) {
ans += 1;
if ((long long)i * i < n) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = 0;
}
}
}
}
return ans;
}
};
207. 课程表
题干
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
- 例如,先修课程对
[0, 1]表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= 5000prerequisites[i].length == 20 <= ai, bi < numCoursesprerequisites[i]中的所有课程对 互不相同
思路
拓扑排序能遍历所有的节点说明成立,否则不成立
代码
class Solution {
private:
vector<vector<int>> edges;
vector<int> indeg;
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
indeg.resize(numCourses);
for (const auto& info: prerequisites) {
edges[info[1]].push_back(info[0]);
++indeg[info[0]];
}
queue<int> q;
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
int visited = 0;
while (!q.empty()) {
++visited;
int u = q.front();
q.pop();
for (int v: edges[u]) {
--indeg[v];
if (indeg[v] == 0) {
q.push(v);
}
}
}
return visited == numCourses;
}
};
208. 实现 Trie (前缀树)
题干
**Trie**(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie()初始化前缀树对象。void insert(String word)向前缀树中插入字符串word。boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。boolean startsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
提示:
1 <= word.length, prefix.length <= 2000word和prefix仅由小写英文字母组成insert、search和startsWith调用次数 总计 不超过3 * 104次
思路
每个节点数据结构为vector<Trie*> children(26)以及bool isEnd,后者表示是否是叶子节点,insert时如果指针位置为null则创建新节点(这个节点的children都为nullptr),查询时如果查到了isEnd为true的节点则查询成功
代码
class Trie {
private:
vector<Trie*> children;
bool isEnd;
Trie* searchPrefix(string prefix) {
Trie* node = this;
for (char ch : prefix) {
ch -= 'a';
if (node->children[ch] == nullptr) {
return nullptr;
}
node = node->children[ch];
}
return node;
}
public:
Trie() : children(26), isEnd(false) {}
~Trie() {
for (auto &child : this->children) {
if (child != nullptr) delete child;
}
}
void insert(string word) {
Trie* node = this;
for (char ch : word) {
ch -= 'a';
if (node->children[ch] == nullptr) {
node->children[ch] = new Trie();
}
node = node->children[ch];
}
node->isEnd = true;
}
bool search(string word) {
Trie* node = this->searchPrefix(word);
return node != nullptr && node->isEnd;
}
bool startsWith(string prefix) {
return this->searchPrefix(prefix) != nullptr;
}
};
209. 长度最小的子数组
题干
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 连续
子数组
[numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 105
进阶:
- 如果你已经实现
O(n)时间复杂度的解法, 请尝试设计一个O(n log(n))时间复杂度的解法。
思路
记录前缀和sums,随后枚举子数组的开始值start,用二分法找到第一个大于等于目标值sums[start]+s的位置,更新答案长度,这里可以使用stl的lower_bound函数
代码
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int n = nums.size();
if (n == 0) {
return 0;
}
int ans = INT_MAX;
vector<int> sums(n + 1, 0);
// 为了方便计算,令 size = n + 1
// sums[0] = 0 意味着前 0 个元素的前缀和为 0
// sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
// 以此类推
for (int i = 1; i <= n; i++) {
sums[i] = sums[i - 1] + nums[i - 1];
}
for (int i = 1; i <= n; i++) {
int target = s + sums[i - 1];
auto bound = lower_bound(sums.begin(), sums.end(), target);
if (bound != sums.end()) {
ans = min(ans, static_cast<int>((bound - sums.begin()) - (i - 1)));
}
}
return ans == INT_MAX ? 0 : ans;
}
};
210. 课程表 II
题干
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。
- 例如,想要学习课程
0,你需要先完成课程1,我们用一个匹配来表示:[0,1]。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3:
输入:numCourses = 1, prerequisites = []
输出:[0]
提示:
1 <= numCourses <= 20000 <= prerequisites.length <= numCourses * (numCourses - 1)prerequisites[i].length == 20 <= ai, bi < numCoursesai != bi- 所有
[ai, bi]互不相同
思路
和207. 课程表类似,拓扑排序能覆盖所有节点说明有答案,queue中取front时将答案记录到vector中
代码
class Solution {
private:
// 存储有向图
vector<vector<int>> edges;
// 存储每个节点的入度
vector<int> indeg;
// 存储答案
vector<int> result;
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
edges.resize(numCourses);
indeg.resize(numCourses);
for (const auto& info: prerequisites) {
edges[info[1]].push_back(info[0]);
++indeg[info[0]];
}
queue<int> q;
// 将所有入度为 0 的节点放入队列中
for (int i = 0; i < numCourses; ++i) {
if (indeg[i] == 0) {
q.push(i);
}
}
while (!q.empty()) {
// 从队首取出一个节点
int u = q.front();
q.pop();
// 放入答案中
result.push_back(u);
for (int v: edges[u]) {
--indeg[v];
// 如果相邻节点 v 的入度为 0,就可以选 v 对应的课程了
if (indeg[v] == 0) {
q.push(v);
}
}
}
if (result.size() != numCourses) {
return {};
}
return result;
}
};
211. 添加与搜索单词 - 数据结构设计
题干
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary()初始化词典对象void addWord(word)将word添加到数据结构中,之后可以对它进行匹配bool search(word)如果数据结构中存在字符串与word匹配,则返回true;否则,返回false。word中可能包含一些'.',每个.都可以表示任何一个字母。
示例:
输入:
["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
[[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
输出:
[null,null,null,null,false,true,true,true]
解释:
WordDictionary wordDictionary = new WordDictionary();
wordDictionary.addWord("bad");
wordDictionary.addWord("dad");
wordDictionary.addWord("mad");
wordDictionary.search("pad"); // 返回 False
wordDictionary.search("bad"); // 返回 True
wordDictionary.search(".ad"); // 返回 True
wordDictionary.search("b.."); // 返回 True
提示:
1 <= word.length <= 25addWord中的word由小写英文字母组成search中的word由 ‘.’ 或小写英文字母组成- 最多调用
104次addWord和search
思路
写一个trie树,随后在trie树中实现dfs,遇到”.“可以dfs所有非空孩子,遇到正常的字母就判断该字母位置指针是否为空,返回条件为到达了叶子节点且长度到达string末尾
代码
class Trie{
public:
vector<Trie*> children;
bool isEnd;
Trie() : children(26), isEnd(false) {}
~Trie() {
for (auto &child : this->children) {
if (child != nullptr) delete child;
}
}
void insert(string word){
Trie* node = this;
for(char ch:word){
if(node->children[ch-'a']!=nullptr){
node = node->children[ch-'a'];
}else{
node->children[ch-'a'] = new Trie();
node = node->children[ch-'a'];
}
}
node->isEnd = true;
}
bool findPrefix(string word,Trie* node,int now){
if(now == word.size()){
if(node->isEnd==true){
return true;
}else{
return false;
}
}
char ch = word[now];
if(ch=='.'){
for(int i=0;i<26;i++){
if(node->children[i]!=nullptr){
if(findPrefix(word, node->children[i], now+1)){
return true;
}
}
}
return false;
}else if(node->children[ch-'a']==nullptr){
return false;
}
return findPrefix(word, node->children[ch-'a'], now+1);
}
};
class WordDictionary {
public:
Trie t;
WordDictionary() {
}
void addWord(string word) {
t.insert(word);
}
bool search(string word) {
return t.findPrefix(word,&t,0);
}
};
/**
* Your WordDictionary object will be instantiated and called as such:
* WordDictionary* obj = new WordDictionary();
* obj->addWord(word);
* bool param_2 = obj->search(word);
*/
213. 打家劫舍 II
题干
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3
提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
思路
同打家劫舍,分类讨论nums[0]取或者不取,截取两个子数组做两遍打家劫舍取最大值
代码
class Solution {
public:
int rob(vector<int>& nums) {
vector<int> dp1(nums.size());
vector<int> dp2(nums.size());
int ans=-1;
if(nums.size()==1) return nums[0];
if(nums.size()==2) return max(nums[0],nums[1]);
dp1[0]=nums[0];
if(dp1[0]>ans) ans = dp1[0];
dp1[1]=max(nums[0],nums[1]);
if(dp1[1]>ans) ans = dp1[1];
for(int i=2;i<nums.size()-1;i++){
dp1[i]=max(dp1[i-2]+nums[i],dp1[i-1]);
if(dp1[i]>ans) ans = dp1[i];
}
dp2[1]=nums[1];
if(dp2[1]>ans) ans = dp2[1];
dp2[2]=max(nums[1],nums[2]);
if(dp2[2]>ans) ans = dp2[2];
for(int i=3;i<nums.size();i++){
dp2[i]=max(dp2[i-2]+nums[i],dp2[i-1]);
if(dp2[i]>ans) ans = dp2[i];
}
return ans;
}
};
215. 数组中的第K个最大元素
题干
给定整数数组 nums 和整数 k,请返回数组中第 **k** 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
提示:
1 <= k <= nums.length <= 105-104 <= nums[i] <= 104
思路
堆的打卡题,会用priority_queue即可
代码
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int> pq;
for(auto &x:nums){
pq.emplace(x);
}
for(int i=0;i<k-1;i++){
pq.pop();
}
return pq.top();
}
};
216. 组合总和 III
题干
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
- 只使用数字1到9
- 每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。
示例 2:
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。
示例 3:
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字,我们可以得到的最小和是1+2+3+4 = 10,因为10 > 1,没有有效的组合。
提示:
2 <= k <= 91 <= n <= 60
思路
dfs题,每个数分为取或者不取,结束条件为k和n都等于0
代码
class Solution {
public:
vector<vector<int>> combinationSum3(int k, int n) {
vector<int> nums = {1,2,3,4,5,6,7,8,9};
int length = nums.size();
vector<vector<int>> answer;
vector<int> temp;
function<void(int,int,int)> dfs = [&](int idx,int k,int n){
if(k==0&&n==0){
answer.emplace_back(temp);
return;
}
if(n<0){
return;
}
if(idx>=length){
return;
}
//不取
dfs(idx+1,k,n);
//取
temp.emplace_back(nums[idx]);
dfs(idx+1,k-1,n-nums[idx]);
temp.pop_back();
};
dfs(0,k,n);
return answer;
}
};
221. 最大正方形
题干
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
示例 1:

输入:matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出:4
示例 2:

输入:matrix = [["0","1"],["1","0"]]
输出:1
示例 3:
输入:matrix = [["0"]]
输出:0
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 300matrix[i][j]为'0'或'1'
思路
二维动态规划,dp[i][j]表示以ij位置为右下角的最大正方形的边长,其和上、左、左上三个相邻的dp值有关,转移方程为
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
代码
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return 0;
}
int maxSide = 0;
int rows = matrix.size(), columns = matrix[0].size();
vector<vector<int>> dp(rows, vector<int>(columns));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < columns; j++) {
if (matrix[i][j] == '1') {
if (i == 0 || j == 0) {
dp[i][j] = 1;
} else {
dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
maxSide = max(maxSide, dp[i][j]);
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
};
223. 矩形面积
题干
给你 二维 平面上两个 由直线构成且边与坐标轴平行/垂直 的矩形,请你计算并返回两个矩形覆盖的总面积。
每个矩形由其 左下 顶点和 右上 顶点坐标表示:
- 第一个矩形由其左下顶点
(ax1, ay1)和右上顶点(ax2, ay2)定义。 - 第二个矩形由其左下顶点
(bx1, by1)和右上顶点(bx2, by2)定义。
示例 1:

输入:ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出:45
示例 2:
输入:ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
输出:16
提示:
-104 <= ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 <= 104
思路
直接用两个矩形面积减去重叠部分面积即可
注意用max和min去求重叠面积,这样不用枚举各个情况
int overlapWidth = min(ax2, bx2) - max(ax1, bx1), overlapHeight = min(ay2, by2) - max(ay1, by1);
代码
class Solution {
public:
int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
int area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
int overlapWidth = min(ax2, bx2) - max(ax1, bx1), overlapHeight = min(ay2, by2) - max(ay1, by1);
int overlapArea = max(overlapWidth, 0) * max(overlapHeight, 0);
return area1 + area2 - overlapArea;
}
};
227. 基本计算器 II
题干
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 [-231, 231 - 1] 的范围内。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
示例 1:
输入:s = "3+2*2"
输出:7
示例 2:
输入:s = " 3/2 "
输出:1
示例 3:
输入:s = " 3+5 / 2 "
输出:5
提示:
1 <= s.length <= 3 * 105s由整数和算符('+', '-', '*', '/')组成,中间由一些空格隔开s表示一个 有效表达式- 表达式中的所有整数都是非负整数,且在范围
[0, 231 - 1]内 - 题目数据保证答案是一个 32-bit 整数
思路
栈中存数值,用一个符号char表示当前符号分类讨论(需要提前设置一个符号‘+’)
代码
class Solution {
public:
int calculate(string s) {
vector<int> st;
int n = s.size();
int preSign = '+';
int num = 0;
int i=0;
int temp;
while(i<n){
if(s[i]>='0'&&s[i]<='9'){
num = num*10+int(s[i]-'0');
}
if((!(s[i]>='0'&&s[i]<='9')&&s[i]!=' ')||i==n-1){
switch(preSign){
case '+':
st.push_back(num);
break;
case '-':
st.push_back(-num);
break;
case '*':
temp = st.back();
st.pop_back();
st.push_back(temp*num);
break;
case '/':
temp = st.back();
st.pop_back();
st.push_back(temp/num);
break;
default:
break;
}
preSign = s[i];
num = 0;
}
i++;
}
return accumulate(st.begin(),st.end(),0);
}
};
229. 多数元素 II
题干
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
示例 1:
输入:nums = [3,2,3]
输出:[3]
示例 2:
输入:nums = [1]
输出:[1]
示例 3:
输入:nums = [1,2]
输出:[1,2]
提示:
1 <= nums.length <= 5 * 104-109 <= nums[i] <= 109
进阶:尝试设计时间复杂度为 O(n)、空间复杂度为 O(1)的算法解决此问题。
思路
俄罗斯方块思想,设置两个num1,num2,再用size1、size2分别记录两个num的出现次数,如果发现访问了第三个数和num1、num2都不同则触发三消,如果数字已经存在则对应size++
代码
class Solution {
public:
vector<int> majorityElement(vector<int>& nums) {
int num1 = 0;
int size1 = 0;
int num2 = 0;
int size2 = 0;
for(int i=0;i<nums.size();i++){
if(size1>0&&nums[i]==num1){
size1++;
}else if(size2>0&&nums[i]==num2){
size2++;
}else if(size1>0&&size2>0&&num1!=nums[i]&&num2!=nums[i]){
size1--;
size2--;
}else{
if(size1==0){
num1 = nums[i];
size1++;
}else if(size2==0){
num2 = nums[i];
size2++;
}
}
}
vector<int> answer;
int n = nums.size();
//num1和num2是潜在答案,需要验证
int cnt1 = 0;
int cnt2 = 0;
for(int i=0;i<nums.size();i++){
if(size1>0&&nums[i]==num1){
cnt1++;
}else if(size2>0&&nums[i]==num2){
cnt2++;
}
}
if(size1>0&&cnt1>n/3){
answer.push_back(num1);
}
if(size2>0&&cnt2>n/3){
answer.push_back(num2);
}
return answer;
}
};
230. 二叉搜索树中第K小的元素
题干
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:

输入:root = [3,1,4,null,2], k = 1
输出:1
示例 2:

输入:root = [5,3,6,2,4,null,null,1], k = 3
输出:3
提示:
- 树中的节点数为
n。 1 <= k <= n <= 1040 <= Node.val <= 104
进阶:如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化算法?
思路
简单一点就直接中序遍历取第k个被遍历,但是考虑到多次频繁调用的情况这一轮不好。因此另一个方法是遍历一次用哈希表存每个节点所包含数字的数量。有了这个哈希表,就可以根据k值和节点左子树的节点数判断这个树是在当前的左子树还是右子树还是根节点了
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class MyBst {
public:
MyBst(TreeNode *root) {
this->root = root;
countNodeNum(root);
}
// 返回二叉搜索树中第k小的元素
int kthSmallest(int k) {
TreeNode *node = root;
while (node != nullptr) {
int left = getNodeNum(node->left);
if (left < k - 1) {
node = node->right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node->left;
}
}
return node->val;
}
private:
TreeNode *root;
unordered_map<TreeNode *, int> nodeNum;
// 统计以node为根结点的子树的结点数
int countNodeNum(TreeNode * node) {
if (node == nullptr) {
return 0;
}
nodeNum[node] = 1 + countNodeNum(node->left) + countNodeNum(node->right);
return nodeNum[node];
}
// 获取以node为根结点的子树的结点数
int getNodeNum(TreeNode * node) {
if (node != nullptr && nodeNum.count(node)) {
return nodeNum[node];
}else{
return 0;
}
}
};
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
MyBst bst(root);
return bst.kthSmallest(k);
}
};
235. 二叉搜索树的最近公共祖先
题干
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉搜索树中。
思路
dfs去做,可以用二叉搜索树的大于小于性质,也可以当成普通的无重复树,找到第一个左边为true右边也为true的节点
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool find;
TreeNode* answer;
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q){
if(!root){
return false;
}
bool left = dfs(root->left,p,q);
bool right = dfs(root->right,p,q);
if(left==true&&right==true){
if(!find){
find = true;
answer = root;
}
return true;
}
if((root==p||root==q)&&(left||right)){
if(!find){
find = true;
answer = root;
}
return true;
}
if(root==p||root==q){
return true;
}
return left||right;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
dfs(root,p,q);
return answer;
}
};
236. 二叉树的最近公共祖先
题干
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
示例 3:
输入:root = [1,2], p = 1, q = 2
输出:1
提示:
- 树中节点数目在范围
[2, 105]内。 -109 <= Node.val <= 109- 所有
Node.val互不相同。 p != qp和q均存在于给定的二叉树中。
思路
dfs找到第一个左边为true右边也为true的节点
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* answer;
int find;
bool dfs(TreeNode* root, TreeNode* p, TreeNode* q){
if(!root){
return false;
}
bool a = dfs(root->left,p,q);
bool b = dfs(root->right,p,q);
if(root==p&&(a|b)&&find==0){
answer = root;
find = 1;
return true;
}
if(root==q&&(a|b)&&find==0){
answer = root;
find = 1;
return true;
}
if(a==true&&b==true&&find==0){
answer = root;
find = 1;
return true;
}
if(a|b){
return true;
}
if(root==p||root==q){
return true;
}
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
find = 0;
dfs(root,p,q);
return answer;
}
};
237. 删除链表中的节点
题干
有一个单链表的 head,我们想删除它其中的一个节点 node。
给你一个需要删除的节点 node 。你将 无法访问 第一个节点 head。
链表的所有值都是 唯一的,并且保证给定的节点 node 不是链表中的最后一个节点。
删除给定的节点。注意,删除节点并不是指从内存中删除它。这里的意思是:
- 给定节点的值不应该存在于链表中。
- 链表中的节点数应该减少 1。
node前面的所有值顺序相同。node后面的所有值顺序相同。
自定义测试:
- 对于输入,你应该提供整个链表
head和要给出的节点node。node不应该是链表的最后一个节点,而应该是链表中的一个实际节点。 - 我们将构建链表,并将节点传递给你的函数。
- 输出将是调用你函数后的整个链表。
示例 1:
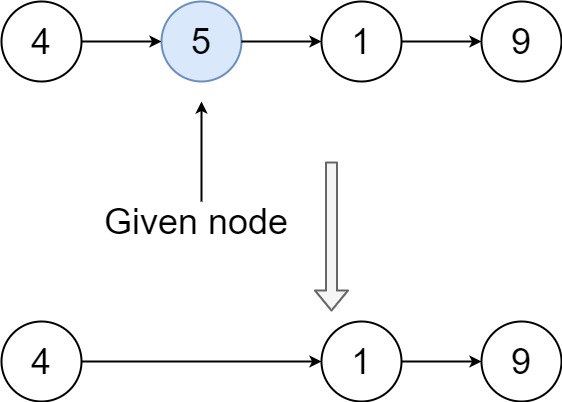
输入:head = [4,5,1,9], node = 5
输出:[4,1,9]
解释:指定链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9
示例 2:
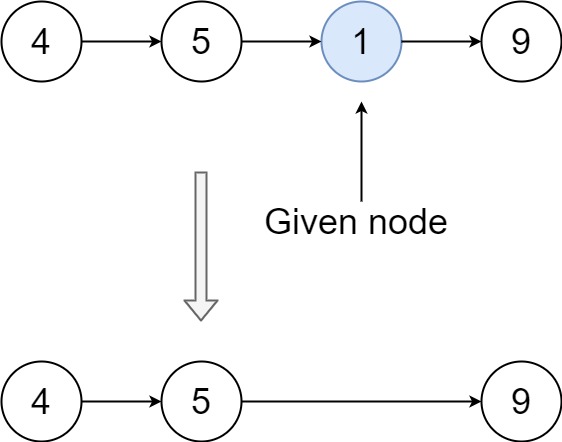
输入:head = [4,5,1,9], node = 1
输出:[4,5,9]
解释:指定链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9
提示:
- 链表中节点的数目范围是
[2, 1000] -1000 <= Node.val <= 1000- 链表中每个节点的值都是 唯一 的
- 需要删除的节点
node是 链表中的节点 ,且 不是末尾节点
思路
直接将下一个节点内容复制到本节点,再删除下一个节点
代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
void deleteNode(ListNode* node) {
ListNode* temp = node;
temp->val = temp->next->val;
temp->next = temp->next->next;
return;
}
};
238. 除自身以外数组的乘积
题干
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(*n*) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105-30 <= nums[i] <= 30- 保证 数组
nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
进阶:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
思路
不能用除法,维护两个dp数组前缀积后缀积,再遍历一次数组输出每个位置前缀积后缀积之积即可
代码
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
// L 和 R 分别表示左右两侧的乘积列表
vector<int> L(length, 0), R(length, 0);
vector<int> answer(length);
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
};
240. 搜索二维矩阵 II
题干
编写一个高效的算法来搜索 *m* x *n* 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出:true
示例 2:
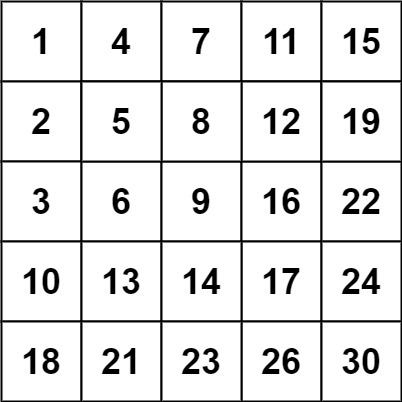
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
思路
对每行进行二分查找,注意lower_bound的使用
代码
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
for (const auto& row: matrix) {
auto it = lower_bound(row.begin(), row.end(), target);
if (it != row.end() && *it == target) {
return true;
}
}
return false;
}
};
241. 为运算表达式设计优先级
题干
给你一个由数字和运算符组成的字符串 expression ,按不同优先级组合数字和运算符,计算并返回所有可能组合的结果。你可以 按任意顺序 返回答案。
生成的测试用例满足其对应输出值符合 32 位整数范围,不同结果的数量不超过 104 。
示例 1:
输入:expression = "2-1-1"
输出:[0,2]
解释:
((2-1)-1) = 0
(2-(1-1)) = 2
示例 2:
输入:expression = "2*3-4*5"
输出:[-34,-14,-10,-10,10]
解释:
(2*(3-(4*5))) = -34
((2*3)-(4*5)) = -14
((2*(3-4))*5) = -10
(2*((3-4)*5)) = -10
(((2*3)-4)*5) = 10
提示:
1 <= expression.length <= 20expression由数字和算符'+'、'-'和'*'组成。- 输入表达式中的所有整数值在范围
[0, 99]
思路
暴力dfs,每次遇到一个符号,就dfs其两侧的子串的两个结果vector,再对这个vector两两组合得到可能答案,当子串为纯数字时则返回数字
代码
class Solution {
public:
vector<int> diffWaysToCompute(string expression) {
vector<int> answer;
function<vector<int>(int,int)> dfs = [&](int l,int r){
vector<int> tmp;
for(int i=l;i<r;i++){
if(expression[i]>='0'&&expression[i]<='9'){
continue;
}
vector<int> left = dfs(l,i-1);
vector<int> right = dfs(i+1,r);
for(int j=0;j<left.size();j++){
for(int k=0;k<right.size();k++){
if(expression[i]=='+'){
tmp.emplace_back(left[j]+right[k]);
}else if(expression[i]=='-'){
tmp.emplace_back(left[j]-right[k]);
}else if(expression[i]=='*'){
tmp.emplace_back(left[j]*right[k]);
}
}
}
}
if(tmp.size()==0){
int num = 0;
for(int j=l;j<=r;j++){
num = num*10+(expression[j]-'0');
}
tmp.emplace_back(num);
}
return tmp;
};
return dfs(0,expression.size()-1);
}
};
244. 最短单词距离 II
题干
请设计一个类,使该类的构造函数能够接收一个字符串数组。然后再实现一个方法,该方法能够分别接收两个单词,并返回列表中这两个单词之间的最短距离。
实现 WordDistanc 类:
WordDistance(String[] wordsDict)用字符串数组wordsDict初始化对象。int shortest(String word1, String word2)返回数组worddict中word1和word2之间的最短距离。
示例 1:
输入:
["WordDistance", "shortest", "shortest"]
[[["practice", "makes", "perfect", "coding", "makes"]], ["coding", "practice"], ["makes", "coding"]]
输出:
[null, 3, 1]
解释:
WordDistance wordDistance = new WordDistance(["practice", "makes", "perfect", "coding", "makes"]);
wordDistance.shortest("coding", "practice"); // 返回 3
wordDistance.shortest("makes", "coding"); // 返回 1
注意:
1 <= wordsDict.length <= 3 * 1041 <= wordsDict[i].length <= 10wordsDict[i]由小写英文字母组成word1和word2在数组wordsDict中word1 != word2shortest操作次数不大于5000
思路
哈希表存每个string的下标数组,然后把两个单词的下标数组找出来,题目转化为求两个数组中数字之差最小,用双指针做即可
代码
class WordDistance {
public:
unordered_map<string,vector<int>> cache;
WordDistance(vector<string>& wordsDict) {
for(int i=0;i<wordsDict.size();i++){
cache[wordsDict[i]].emplace_back(i);
}
}
int shortest(string word1, string word2) {
int answer = INT_MAX;
int index1 = 0;
int index2 = 0;
vector<int> a = cache[word1];
vector<int> b = cache[word2];
while(index1<a.size()&&index2<b.size()){
answer = min(answer,abs(a[index1]-b[index2]));
if(a[index1]>b[index2]){
index2++;
}else{
index1++;
}
}
return answer;
}
};
/**
* Your WordDistance object will be instantiated and called as such:
* WordDistance* obj = new WordDistance(wordsDict);
* int param_1 = obj->shortest(word1,word2);
*/
245. 最短单词距离 III
题干
给定一个字符串数组 wordsDict 和两个字符串 word1 和 word2 ,返回这两个单词在列表中出现的最短距离。
注意:word1 和 word2 是有可能相同的,并且它们将分别表示为列表中 两个独立的单词 。
示例 1:
输入:wordsDict = ["practice", "makes", "perfect", "coding", "makes"], word1 = "makes", word2 = "coding"
输出:1
示例 2:
输入:wordsDict = ["practice", "makes", "perfect", "coding", "makes"], word1 = "makes", word2 = "makes"
输出:3
提示:
1 <= wordsDict.length <= 1051 <= wordsDict[i].length <= 10wordsDict[i]由小写英文字母组成word1和word2都在wordsDict中
思路
哈希表存每个string的下标数组,然后把两个单词的下标数组找出来,题目转化为求两个数组中数字之差最小,用双指针做即可。如果是相同的单词,则改为求这个单词相邻数最小差
代码
class Solution {
public:
unordered_map<string,vector<int>> mp;
int same_word(vector<int> &v){
int answer = INT_MAX;
for(int i=0;i<v.size()-1;i++){
answer = min(answer,v[i+1]-v[i]);
}
return answer;
}
int two_words(vector<int> &v1,vector<int> &v2){
int idx1 = 0;
int idx2 = 0;
int size1 = v1.size();
int size2 = v2.size();
int answer = INT_MAX;
while(idx1<size1&&idx2<size2){
answer = min(answer,abs(v1[idx1]-v2[idx2]));
if(v1[idx1]>v2[idx2]){
idx2++;
}else{
idx1++;
}
}
return answer;
}
int shortestWordDistance(vector<string>& wordsDict, string word1, string word2) {
for(int i=0;i<wordsDict.size();i++){
mp[wordsDict[i]].emplace_back(i);
}
vector<int> w1 = mp[word1];
vector<int> w2 = mp[word2];
if(word1==word2){
return same_word(w1);
}
return two_words(w1, w2);
};
};
247. 中心对称数 II
题干
给定一个整数 n ,返回所有长度为 n 的 中心对称数 。你可以以 任何顺序 返回答案。
中心对称数 是一个数字在旋转了 180 度之后看起来依旧相同的数字(或者上下颠倒地看)。
示例 1:
输入:n = 2
输出:["11","69","88","96"]
示例 2:
输入:n = 1
输出:["0","1","8"]
提示:
1 <= n <= 14
思路
哈希表或者数组存对称字符组的对应关系以及单个对称字符,dfs一半长度的字符串即可,注意奇偶分类奇数的话要枚举中间数,还有一个坑是第一项不能为0
代码
class Solution {
public:
vector<string> findStrobogrammatic(int n) {
vector<vector<char>> pairs = {{'0','0'},{'1','1'},{'6','9'},{'8','8'},{'9','6'}};
vector<string> single = {"0","1","8"};
vector<string> answer;
string s1 ="";
string s2 ="";
int length = n/2;
int hasSingle = n%2;
function<void(int)> dfs = [&](int i){
//cout<<i<<endl;
if(i==length){
string s3 = s2;
reverse(s3.begin(), s3.end());
if(hasSingle==0){
answer.emplace_back(s1+s3);
}else{
for(int k=0;k<3;k++){
//cout<<s1+single[k]+s3<<endl;
answer.emplace_back(s1+single[k]+s3);
}
}
return;
}
if(i!=0){
s1.push_back(pairs[0][0]);
s2.push_back(pairs[0][1]);
dfs(i+1);
s1.pop_back();
s2.pop_back();
}
for(int j=1;j<5;j++){
s1.push_back(pairs[j][0]);
s2.push_back(pairs[j][1]);
dfs(i+1);
s1.pop_back();
s2.pop_back();
}
};
dfs(0);
return answer;
}
};
250. 统计同值子树
题干
给定一个二叉树,统计该二叉树数值相同的
子树
个数。
同值子树是指该子树的所有节点都拥有相同的数值。
示例:
输入: root = [5,1,5,5,5,null,5]
5
/ \
1 5
/ \ \
5 5 5
输出: 4
思路
树的dfs题,前向遍历,每个节点判断当前节点为根节点的树是否为同值子树即可
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int answer;
bool dfs(TreeNode* root){
if(!root->left&&!root->right){
answer++;
return true;
}
bool isTrue = true;
if(root->left){
if(dfs(root->left)==false){
isTrue = false;
}
if(root->val!=root->left->val){
isTrue = false;
}
}
if(root->right){
if(dfs(root->right)==false){
isTrue = false;
}
if(root->val!=root->right->val){
isTrue = false;
}
}
if(isTrue){
answer++;
}
return isTrue;
}
int countUnivalSubtrees(TreeNode* root) {
if(!root){
return 0;
}
answer = 0;
dfs(root);
return answer;
}
};
251. 展开二维向量
题干
请设计并实现一个能够展开二维向量的迭代器。该迭代器需要支持 next 和 hasNext 两种操作。
示例:
Vector2D iterator = new Vector2D([[1,2],[3],[4]]);
iterator.next(); // 返回 1
iterator.next(); // 返回 2
iterator.next(); // 返回 3
iterator.hasNext(); // 返回 true
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 4
iterator.hasNext(); // 返回 false
注意:
- 请记得 重置 在 Vector2D 中声明的类变量(静态变量),因为类变量会 在多个测试用例中保持不变,影响判题准确。请 查阅 这里。
- 你可以假定
next()的调用总是合法的,即当next()被调用时,二维向量总是存在至少一个后续元素。
进阶:尝试在代码中仅使用 C++ 提供的迭代器 或 Java 提供的迭代器。
思路
维护inner和outer两个指针即可outer指向第outer个vector<int>,inner是该vector的内部指针,outer < vec.size() && inner == vec[outer].size()这句来判断是否应该移动outer
代码
class Vector2D {
public:
Vector2D(vector<vector<int>>& vec) {
this->vec = vec;
}
int next() {
advanceToNext();
// 返回当前元素并向内移动,使其位于当前元素之后。
return vec[outer][inner++];
}
// 如果当前 outer 和 internal 指向一个整数,则此方法不执行任何操作。
// 否则,内部和外部将向前推进,直到它们指向一个整数。
// 如果没有更多的整数,则当此方法终止时,outer 将等于 vector.length。
void advanceToNext() {
// 虽然 outer 仍然在向量内,但 internal 位于 outer 指向的 internal 列表的末尾,
// 我们希望向前移动到下一个 internal 向量的起点。
while (outer < vec.size() && inner == vec[outer].size()) {
inner = 0;
outer++;
}
}
bool hasNext() {
// 确保移动位置指针以使其指向整数,
// 或者让 outer = vector.length.
advanceToNext();
// 如果 outer = vector.length 那么就没有剩下的整数了,
// 否则我们会在一个整数停下,也就是还有剩下的整数。
return outer < vec.size();
}
private:
vector<vector<int>> vec;
int inner = 0;
int outer = 0;
};
/**
* Your Vector2D object will be instantiated and called as such:
* Vector2D* obj = new Vector2D(vec);
* int param_1 = obj->next();
* bool param_2 = obj->hasNext();
*/
253. 会议室 II
题干
给你一个会议时间安排的数组 intervals ,每个会议时间都会包括开始和结束的时间 intervals[i] = [starti, endi] ,返回 所需会议室的最小数量 。
示例 1:
输入:intervals = [[0,30],[5,10],[15,20]]
输出:2
示例 2:
输入:intervals = [[7,10],[2,4]]
输出:1
提示:
1 <= intervals.length <= 1040 <= starti < endi <= 106
思路
贪心堆,用堆维护会议室结束时间,堆的大小即为会议室个数,我们尝试每次让一个新会议加入结束最早的会议室,如果能找到则pop并push一个新的结束时间,否则直接新建一个会议室
代码
class Solution {
public:
int minMeetingRooms(vector<vector<int>>& intervals) {
auto cmp = [&](const vector<int> &a,const vector<int> &b){
if(a[0]==b[0]){
return a[1]<b[1];
}
return a[0]<b[0];
};
sort(intervals.begin(), intervals.end(), cmp);
auto cmp2 = [&](const int& a,const int& b){
return a>=b;
};
priority_queue<int, vector<int>, decltype(cmp2)> pq(cmp2);
pq.emplace(intervals[0][1]);
for(int i=1;i<intervals.size();i++){
if(intervals[i][0]>=pq.top()){
pq.pop();
}
pq.emplace(intervals[i][1]);
}
return pq.size();
}
};
254. 因子的组合
题干
整数可以被看作是其因子的乘积。
例如:
8 = 2 x 2 x 2;
= 2 x 4.
请实现一个函数,该函数接收一个整数 n 并返回该整数所有的因子组合。
注意:
- 你可以假定 n 为永远为正数。
- 因子必须大于 1 并且小于 n。
示例 1:
输入: 1
输出: []
示例 2:
输入: 37
输出: []
示例 3:
输入: 12
输出:
[
[2, 6],
[2, 2, 3],
[3, 4]
]
示例 4:
输入: 32
输出:
[
[2, 16],
[2, 2, 8],
[2, 2, 2, 4],
[2, 2, 2, 2, 2],
[2, 4, 4],
[4, 8]
]
思路
dfs枚举因子,随后暴力回溯,注意每次递归时的k具有非减性
代码
class Solution {
public:
vector<vector<int>> getFactors(int n) {
vector<vector<int>> answer;
vector<int> temp;
function<void(int,int)> dfs = [&](int n,int k){
for(int i=k;i<=sqrt(n);i++){
if(n%i==0){
temp.emplace_back(i);
temp.emplace_back(n/i);
answer.emplace_back(temp);
temp.pop_back();
dfs(n/i,i);
temp.pop_back();
}
}
};
dfs(n,2);
return answer;
}
};
255. 验证二叉搜索树的前序遍历序列
题干
给定一个 无重复元素 的整数数组 preorder , 如果它是以二叉搜索树的先序遍历排列 ,返回 true 。
示例 1:
输入: preorder = [5,2,1,3,6]
输出: true
示例 2:
输入: preorder = [5,2,6,1,3]
输出: false
提示:
1 <= preorder.length <= 1041 <= preorder[i] <= 104preorder中 无重复元素
进阶:您能否使用恒定的空间复杂度来完成此题?
思路
递归,preorder的第一个数是根节点,又由于是二叉搜索树,将剩余数组分为小于根节点和大于根节点的两部分,分别进行子问题dfs
代码
class Solution {
public:
bool dfs(vector<int>& preorder,int start,int end){
if(start>=end){
return true;
}
int now = preorder[start];
int i;
for(i=start+1;i<=end;i++){
if(now<preorder[i]){
break;
}
}
for(int j=i;j<=end;j++){
if(now>preorder[j]){
return false;
}
}
bool left = dfs(preorder,start+1,i-1);
bool right = dfs(preorder,i,end);
return left&&right;
};
bool verifyPreorder(vector<int>& preorder) {
return dfs(preorder,0,preorder.size()-1);
}
};
256. 粉刷房子
题干
假如有一排房子,共 n 个,每个房子可以被粉刷成红色、蓝色或者绿色这三种颜色中的一种,你需要粉刷所有的房子并且使其相邻的两个房子颜色不能相同。
当然,因为市场上不同颜色油漆的价格不同,所以房子粉刷成不同颜色的花费成本也是不同的。每个房子粉刷成不同颜色的花费是以一个 n x 3 的正整数矩阵 costs 来表示的。
例如,costs[0][0] 表示第 0 号房子粉刷成红色的成本花费;costs[1][2] 表示第 1 号房子粉刷成绿色的花费,以此类推。
请计算出粉刷完所有房子最少的花费成本。
示例 1:
输入: costs = [[17,2,17],[16,16,5],[14,3,19]]
输出: 10
解释: 将 0 号房子粉刷成蓝色,1 号房子粉刷成绿色,2 号房子粉刷成蓝色。
最少花费: 2 + 5 + 3 = 10。
示例 2:
输入: costs = [[7,6,2]]
输出: 2
提示:
costs.length == ncosts[i].length == 31 <= n <= 1001 <= costs[i][j] <= 20
思路
二维动态规划,012表示三种颜色,dp[i][0] = costs[i][0]+min(dp[i-1][1],dp[i-1][2]);其余两种颜色的转移方程类似
代码
class Solution {
public:
int minCost(vector<vector<int>>& costs) {
vector<vector<int>> dp(costs.size(),vector<int>(3));
dp[0][0] = costs[0][0];
dp[0][1] = costs[0][1];
dp[0][2] = costs[0][2];
for(int i=1;i<costs.size();i++){
dp[i][0] = costs[i][0]+min(dp[i-1][1],dp[i-1][2]);
dp[i][1] = costs[i][1]+min(dp[i-1][0],dp[i-1][2]);
dp[i][2] = costs[i][2]+min(dp[i-1][0],dp[i-1][1]);
}
return min(dp[costs.size()-1][0],min(dp[costs.size()-1][1],dp[costs.size()-1][2]));
}
};
259. 较小的三数之和
题干
给定一个长度为 n 的整数数组和一个目标值 target ,寻找能够使条件 nums[i] + nums[j] + nums[k] < target 成立的三元组 i, j, k 个数(0 <= i < j < k < n)。
示例 1:
输入: nums = [-2,0,1,3], target = 2
输出: 2
解释: 因为一共有两个三元组满足累加和小于 2:
[-2,0,1]
[-2,0,3]
示例 2:
输入: nums = [], target = 0
输出: 0
示例 3:
输入: nums = [0], target = 0
输出: 0
提示:
n == nums.length0 <= n <= 3500-100 <= nums[i] <= 100-100 <= target <= 100
思路
类似三数之和,但不是相等而是小于target,先确定第一个值,再用双指针,用双指针时候先固定右指针,再移动左指针,每次答案添加end-start
代码
class Solution {
public:
int threeSumSmaller(vector<int>& nums, int target) {
sort(nums.begin(),nums.end());
int answer = 0;
int n = nums.size();
for(int i=0;i<n-2;i++){
int a = nums[i];
int t = target-a;
int start = i+1;
int end = n-1;
while(start<end){
if(nums[start]+nums[end]<t){
answer+=end-start;
start++;
}else{
end--;
}
}
}
return answer;
}
};
260. 只出现一次的数字 III
题干
给你一个整数数组 nums,其中恰好有两个元素只出现一次,其余所有元素均出现两次。 找出只出现一次的那两个元素。你可以按 任意顺序 返回答案。
你必须设计并实现线性时间复杂度的算法且仅使用常量额外空间来解决此问题。
示例 1:
输入:nums = [1,2,1,3,2,5]
输出:[3,5]
解释:[5, 3] 也是有效的答案。
示例 2:
输入:nums = [-1,0]
输出:[-1,0]
示例 3:
输入:nums = [0,1]
输出:[1,0]
提示:
2 <= nums.length <= 3 * 104-231 <= nums[i] <= 231 - 1- 除两个只出现一次的整数外,
nums中的其他数字都出现两次
思路
用全部数字异或得到两个唯一数字的异或结果xor_all(其余成对的都变0了),再取这个xor_all的最低位的1,将数字分成两类分别异或
代码
class Solution {
public:
vector<int> singleNumber(vector<int> &nums) {
unsigned int xor_all = 0;
for (int x: nums) {
xor_all ^= x;
}
int lowbit = xor_all & -xor_all;//记忆
vector<int> ans(2);
for (int x: nums) {
ans[(x & lowbit) != 0] ^= x; // 分组异或
}
return ans;
}
};
261. 以图判树
题干
给定编号从 0 到 n - 1 的 n 个结点。给定一个整数 n 和一个 edges 列表,其中 edges[i] = [ai, bi] 表示图中节点 ai 和 bi 之间存在一条无向边。
如果这些边能够形成一个合法有效的树结构,则返回 true ,否则返回 false 。
示例 1:
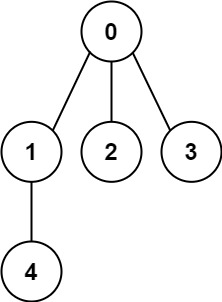
输入: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
输出: true
示例 2:
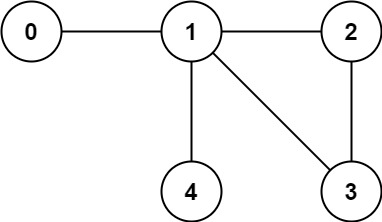
输入: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
输出: false
提示:
1 <= n <= 20000 <= edges.length <= 5000edges[i].length == 20 <= ai, bi < nai != bi- 不存在自循环或重复的边
思路
if (edges.size() != n - 1) return false排除有环的情况,随后dfs遍历记录visit数组,排除节点单独分离的情况
代码
class Solution {
vector<vector<int>> adjacency; // unordered_map<int, vector<int>> adjacency;
set<int> visited;
public:
bool validTree(int n, vector<vector<int>>& edges) {
if (edges.size() != n - 1) return false; // 很关键,排除了同时【连通和有环的】情况
this->adjacency.resize(n);
for (auto& edge : edges) {
adjacency[edge[0]].push_back(edge[1]);
adjacency[edge[1]].push_back(edge[0]);
}
dfs(0);
return visited.size() == n;
}
void dfs(int i) {
visited.insert(i);
for (auto& adj : adjacency[i]) {
if (!visited.contains(adj)) {
dfs(adj);
}
}
}
};
264. 丑数 II
题干
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
丑数 就是质因子只包含 2、3 和 5 的正整数。
示例 1:
输入:n = 10
输出:12
解释:[1, 2, 3, 4, 5, 6, 8, 9, 10, 12] 是由前 10 个丑数组成的序列。
示例 2:
输入:n = 1
输出:1
解释:1 通常被视为丑数。
提示:
1 <= n <= 1690
思路
堆加哈希表,堆用来排序,哈希表用来排除重复值
代码
class Solution {
public:
vector<int> key = {2,3,5};
int nthUglyNumber(int n) {
auto cmp = [&](const long long a,const long long b){
return a>b;
};
unordered_set<long long> set;
priority_queue<long long,vector<long long>,decltype(cmp)> pq(cmp);
int k=n;
pq.push(1);
int answer;
while(k>0){
if(pq.empty()){
break;
}
long long temp = pq.top();
pq.pop();
k--;
if(k==0){
answer = temp;
break;
}
for(int i=0;i<key.size();i++){
if(set.count(temp*key[i])==0){
pq.push(temp*key[i]);
set.insert(temp*key[i]);
}
}
}
return answer;
}
};
267. 回文排列 II
题干
给定一个字符串 s ,返回 其重新排列组合后可能构成的所有回文字符串,并去除重复的组合 。
你可以按 任意顺序 返回答案。如果 s 不能形成任何回文排列时,则返回一个空列表。
示例 1:
输入: s = "aabb"
输出: ["abba", "baab"]
示例 2:
输入: s = "abc"
输出: []
提示:
1 <= s.length <= 16s仅由小写英文字母组成
思路
哈希表计数,如果能成回文排列,则取其一半,利用全排列的做法得到一半string的所有的全排列,再拼接另一半
代码
class Solution {
public:
bool hasSingle;
char single;
vector<string> generatePalindromes(string s) {
hasSingle = false;
single = '\0';
vector<int> mp(26);
int n = s.size();
for(int i=0;i<n;i++){
mp[s[i]-'a']++;
}
if(!check(mp)){
return {};
}
string x ="";
for(int i=0;i<26;i++){
for(int j=0;j<mp[i]/2;j++){
x+='a'+i;
}
}
vector<string> halfAnswer = permutation(x);
vector<string> answer;
if(s.size()==1){
answer.emplace_back(s);
return answer;
}
for(auto &x:halfAnswer){
string temp = x;
reverse(temp.begin(), temp.end());
string temp2 = x;
if(hasSingle){
temp2+=single;
}
temp2+=temp;
answer.emplace_back(temp2);
}
return answer;
};
bool check(vector<int> &v){
for(int i=0;i<v.size();i++){
if(v[i]%2==1){
if(hasSingle){
return false;
}else{
hasSingle = true;
single = 'a'+i;
}
}
}
return true;
}
vector<string> permutation(string x){
vector<string> answer;
string s = x;
int n = x.size();
function<void(int)> dfs = [&](int i){
if(i==n-1){
answer.emplace_back(s);
}
unordered_set<int> st;
for(int k=i;k<n;k++){
//如果这一轮交换重复则跳过
if(st.count(s[k])){
continue;
}
st.insert(s[k]);
swap(s[i],s[k]);
dfs(i+1);
swap(s[i],s[k]);
}
};
dfs(0);
return answer;
};
};
271. 字符串的编码与解码
题干
请你设计一个算法,可以将一个 字符串列表 编码成为一个 字符串。这个编码后的字符串是可以通过网络进行高效传送的,并且可以在接收端被解码回原来的字符串列表。
1 号机(发送方)有如下函数:
string encode(vector<string> strs) {
// ... your code
return encoded_string;
}
2 号机(接收方)有如下函数:
vector<string> decode(string s) {
//... your code
return strs;
}
1 号机(发送方)执行:
string encoded_string = encode(strs);
2 号机(接收方)执行:
vector<string> strs2 = decode(encoded_string);
此时,2 号机(接收方)的 strs2 需要和 1 号机(发送方)的 strs 相同。
请你来实现这个 encode 和 decode 方法。
注意:
- 因为字符串可能会包含 256 个合法 ascii 字符中的任何字符,所以您的算法必须要能够处理任何可能会出现的字符。
- 请勿使用 “类成员”、“全局变量” 或 “静态变量” 来存储这些状态,您的编码和解码算法应该是非状态依赖的。
- 请不要依赖任何方法库,例如
eval又或者是serialize之类的方法。本题的宗旨是需要您自己实现 “编码” 和 “解码” 算法。
思路
通过自己定义添加分隔符数字长度进行编码解码
代码
class Codec {
public:
// Encodes a list of strings to a single string.
string encode(vector<string>& strs) {
string answer = "";
for(int i=0;i<strs.size();i++){
int len = strs[i].size();
answer+="["+to_string(len)+"]";
answer+=strs[i];
}
cout<<answer<<endl;
return answer;
}
// Decodes a single string to a list of strings.
vector<string> decode(string s) {
vector<string> answer;
int i = 0;
while(i<s.size()){
int num = 0;
i++;
// cout<<i<<endl;
while(s[i]>='0'&&s[i]<='9'){
num = num*10+s[i]-'0';
i++;
}
i++;
if(num==0){
// cout<<"emplace:"<<i<<endl;
answer.emplace_back("");
}else{
if(i>=s.size()){
break;
}
answer.emplace_back(s.substr(i,num));
}
i = i+num;
}
return answer;
}
};
// Your Codec object will be instantiated and called as such:
// Codec codec;
// codec.decode(codec.encode(strs));
274. H 指数
题干
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值,**h 指数** 是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
示例 2:
输入:citations = [1,3,1]
输出:1
提示:
n == citations.length1 <= n <= 50000 <= citations[i] <= 1000
思路
排序后,从最后往前遍历
代码
class Solution {
public:
int hIndex(vector<int>& citations) {
sort(citations.begin(), citations.end());
int h = 0, i = citations.size() - 1;
while (i >= 0 && citations[i] > h) {
h++;
i--;
}
return h;
}
};
275. H 指数 II
题干
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数,citations 已经按照 升序排列 。计算并返回该研究者的 h 指数。
h 指数的定义:h 代表“高引用次数”(high citations),一名科研人员的 h 指数是指他(她)的 (n 篇论文中)至少 有 h 篇论文分别被引用了至少 h 次。
请你设计并实现对数时间复杂度的算法解决此问题。
示例 1:
输入:citations = [0,1,3,5,6]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 0, 1, 3, 5, 6 次。
由于研究者有3篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3 。
示例 2:
输入:citations = [1,2,100]
输出:2
提示:
n == citations.length1 <= n <= 1050 <= citations[i] <= 1000citations按 升序排列
思路
同274. H 指数如果已经有序则不用排序直接二分
代码
class Solution {
public:
int hIndex(vector<int>& citations) {
int n = citations.size();
int left = 0, right = n - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (citations[mid] >= n - mid) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return n - left;
}
};
276. 栅栏涂色
题干
有 k 种颜色的涂料和一个包含 n 个栅栏柱的栅栏,请你按下述规则为栅栏设计涂色方案:
- 每个栅栏柱可以用其中 一种 颜色进行上色。
- 相邻的栅栏柱 最多连续两个 颜色相同。
给你两个整数 k 和 n ,返回所有有效的涂色 方案数 。
示例 1:
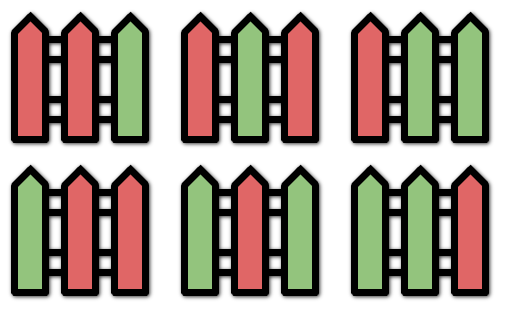
输入:n = 3, k = 2
输出:6
解释:所有的可能涂色方案如上图所示。注意,全涂红或者全涂绿的方案属于无效方案,因为相邻的栅栏柱 最多连续两个 颜色相同。
示例 2:
输入:n = 1, k = 1
输出:1
示例 3:
输入:n = 7, k = 2
输出:42
提示:
1 <= n <= 501 <= k <= 105- 题目数据保证:对于输入的
n和k,其答案在范围[0, 231 - 1]内
思路
动态规划,转移方程为totalWays(i) = (k - 1) * totalWays(i - 1) + (k - 1) * totalWays(i - 2)
代码
class Solution {
public:
int numWays(int n, int k) {
vector<int> dp(n+1);
if(n==1){
return k;
}
if(n==2){
return k*k;
}
dp[1] = k;
dp[2] = k*k;
for(int i=3;i<=n;i++){
dp[i]=dp[i-1]*(k-1)+1*dp[i-2]*(k-1);
}
return dp[n];
}
};
277. 搜寻名人
题干
假设你是一个专业的狗仔,参加了一个 n 人派对,其中每个人被从 0 到 n - 1 标号。在这个派对人群当中可能存在一位 “名人”。所谓 “名人” 的定义是:其他所有 n - 1 个人都认识他/她,而他/她并不认识其他任何人。
现在你想要确认这个 “名人” 是谁,或者确定这里没有 “名人”。而你唯一能做的就是问诸如 “A 你好呀,请问你认不认识 B呀?” 的问题,以确定 A 是否认识 B。你需要在(渐近意义上)尽可能少的问题内来确定这位 “名人” 是谁(或者确定这里没有 “名人”)。
在本题中,你可以使用辅助函数 bool knows(a, b) 获取到 A 是否认识 B。请你来实现一个函数 int findCelebrity(n)。
派对最多只会有一个 “名人” 参加。若 “名人” 存在,请返回他/她的编号;若 “名人” 不存在,请返回 -1。
示例 1:
输入: graph = [
[1,1,0],
[0,1,0],
[1,1,1]
]
输出: 1
解释: 有编号分别为 0、1 和 2 的三个人。graph[i][j] = 1 代表编号为 i 的人认识编号为 j 的人,而 graph[i][j] = 0 则代表编号为 i 的人不认识编号为 j 的人。“名人” 是编号 1 的人,因为 0 和 2 均认识他/她,但 1 不认识任何人。
示例 2:
输入: graph = [
[1,0,1],
[1,1,0],
[0,1,1]
]
输出: -1
解释: 没有 “名人”
提示:
n == graph.lengthn == graph[i].length2 <= n <= 100graph[i][j]是0或1.graph[i][i] == 1
进阶:如果允许调用 API knows 的最大次数为 3 * n ,你可以设计一个不超过最大调用次数的解决方案吗?
思路
排除法,按照顺序相邻节点询问,一开始候选人是0,如果0->1为true说明0肯定不是,候选人变为1,最后再检测候选人是否与其余节点全联通
代码
/* The knows API is defined for you.
bool knows(int a, int b); */
class Solution {
public:
int numberOfPeople;
int findCelebrity(int n) {
numberOfPeople = n;
int celebrityCandidate = 0;
for (int i = 0; i < n; i++) {
if (knows(celebrityCandidate, i)) {
celebrityCandidate = i;
}
}
if (isCelebrity(celebrityCandidate)) {
return celebrityCandidate;
}
return -1;
}
bool isCelebrity(int x){
for(int i=0;i<numberOfPeople;i++){
if(x!=i){
if(knows(x,i)||!knows(i,x)){
return false;
}
}
}
return true;
}
};
279. 完全平方数
题干
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
1 <= n <= 104
思路
一维动态规划,每次枚举遍历当前值减去范围内的完全平方数的那个dp状态
代码
class Solution {
public:
int numSquares(int n) {
vector<int> f(n + 1);
for (int i = 1; i <= n; i++) {
int minn = INT_MAX;
for (int j = 1; j * j <= i; j++) {
minn = min(minn, f[i - j * j]);
}
f[i] = minn + 1;
}
return f[n];
}
};
280. 摆动排序
题干
给你一个的整数数组 nums, 将该数组重新排序后使 nums[0] <= nums[1] >= nums[2] <= nums[3]...
输入数组总是有一个有效的答案。
示例 1:
输入:nums = [3,5,2,1,6,4]
输出:[3,5,1,6,2,4]
解释:[1,6,2,5,3,4]也是有效的答案
示例 2:
输入:nums = [6,6,5,6,3,8]
输出:[6,6,5,6,3,8]
提示:
1 <= nums.length <= 5 * 1040 <= nums[i] <= 104- 输入的
nums保证至少有一个答案。
进阶:你能在 O(n) 时间复杂度下解决这个问题吗?
思路
贪心法进行相邻交换
代码
class Solution {
public:
void swap(vector<int>& nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
void wiggleSort(vector<int>& nums) {
for (int i = 0; i < nums.size() - 1; i++) {
if (((i % 2 == 0) && nums[i] > nums[i + 1]) ||
((i % 2 == 1) && nums[i] < nums[i + 1])) {
swap(nums, i, i + 1);
}
}
}
};
281. 锯齿迭代器
题干
给出两个整数向量 v1 和 v2,请你实现一个迭代器,交替返回它们的元素。
实现 ZigzagIterator 类:
ZigzagIterator(List<int> v1, List<int> v2)用两个向量v1和v2初始化对象。boolean hasNext()如果迭代器还有元素返回true,否则返回false。int next()返回迭代器的当前元素并将迭代器移动到下一个元素。
示例 1:
输入:v1 = [1,2], v2 = [3,4,5,6]
输出:[1,3,2,4,5,6]
解释:通过重复调用 next 直到 hasNext 返回 false,那么 next 返回的元素的顺序应该是:[1,3,2,4,5,6]。
示例 2:
输入:v1 = [1], v2 = []
输出:[1]
示例 3:
输入:v1 = [], v2 = [1]
输出:[1]
拓展:假如给你 k 个向量呢?你的代码在这种情况下的扩展性又会如何呢?
拓展声明:
“锯齿” 顺序对于 k > 2 的情况定义可能会有些歧义。所以,假如你觉得 “锯齿” 这个表述不妥,也可以认为这是一种 “循环”。例如:
输入:v1 = [1,2,3], v2 = [4,5,6,7], v3 = [8,9]
输出:[1,4,8,2,5,9,3,6,7]
思路
用标志位说明当前迭代在哪个vector中
代码
class ZigzagIterator {
public:
vector<int> vt1;
int a1;
vector<int> vt2;
int a2;
int now;
ZigzagIterator(vector<int>& v1, vector<int>& v2) {
vt1 = v1;
vt2 = v2;
a1 = 0;
a2 = 0;
if(v1.size()>0){
now = 0;
}else{
now = 1;
}
}
int next() {
int answer;
if(now==0){
answer = vt1[a1];
a1++;
if(a2<vt2.size()){
now = 1 - now;
}
}else{
answer = vt2[a2];
a2++;
if(a1<vt1.size()){
now = 1 - now;
}
}
return answer;
}
bool hasNext() {
if(now==0){
return a1<vt1.size();
}else{
return a2<vt2.size();
}
}
};
/**
* Your ZigzagIterator object will be instantiated and called as such:
* ZigzagIterator i(v1, v2);
* while (i.hasNext()) cout << i.next();
*/
284. 窥视迭代器
题干
请你在设计一个迭代器,在集成现有迭代器拥有的 hasNext 和 next 操作的基础上,还额外支持 peek 操作。
实现 PeekingIterator 类:
PeekingIterator(Iterator<int> nums)使用指定整数迭代器nums初始化迭代器。int next()返回数组中的下一个元素,并将指针移动到下个元素处。bool hasNext()如果数组中存在下一个元素,返回true;否则,返回false。int peek()返回数组中的下一个元素,但 不 移动指针。
注意:每种语言可能有不同的构造函数和迭代器 Iterator,但均支持 int next() 和 boolean hasNext() 函数。
示例 1:
输入:
["PeekingIterator", "next", "peek", "next", "next", "hasNext"]
[[[1, 2, 3]], [], [], [], [], []]
输出:
[null, 1, 2, 2, 3, false]
解释:
PeekingIterator peekingIterator = new PeekingIterator([1, 2, 3]); // [1,2,3]
peekingIterator.next(); // 返回 1 ,指针移动到下一个元素 [1,2,3]
peekingIterator.peek(); // 返回 2 ,指针未发生移动 [1,2,3]
peekingIterator.next(); // 返回 2 ,指针移动到下一个元素 [1,2,3]
peekingIterator.next(); // 返回 3 ,指针移动到下一个元素 [1,2,3]
peekingIterator.hasNext(); // 返回 False
提示:
1 <= nums.length <= 10001 <= nums[i] <= 1000- 对
next和peek的调用均有效 next、hasNext和peek最多调用1000次
进阶:你将如何拓展你的设计?使之变得通用化,从而适应所有的类型,而不只是整数型?
思路
单独存储下一个变量
代码
class PeekingIterator : public Iterator {
public:
int _next; // 用来存储下一个变量
bool _hasNext; // 存储是否存在下一个元素
PeekingIterator(const vector<int>& nums) : Iterator(nums) {
_hasNext = Iterator::hasNext();
if (_hasNext) _next = Iterator::next();
}
int peek() {
return _next;
}
int next() {
int dummy = _next;
_hasNext = Iterator::hasNext();
if (_hasNext) _next = Iterator::next();
return dummy;
}
bool hasNext() const {
return _hasNext;
}
};
285. 二叉搜索树中的中序后继
题干
给定一棵二叉搜索树和其中的一个节点 p ,找到该节点在树中的中序后继。如果节点没有中序后继,请返回 null 。
节点 p 的后继是值比 p.val 大的节点中键值最小的节点。
示例 1:
输入:root = [2,1,3], p = 1
输出:2
解释:这里 1 的中序后继是 2。请注意 p 和返回值都应是 TreeNode 类型。
示例 2:
输入:root = [5,3,6,2,4,null,null,1], p = 6
输出:null
解释:因为给出的节点没有中序后继,所以答案就返回 null 了。
提示:
- 树中节点的数目在范围
[1, 104]内。 -105 <= Node.val <= 105- 树中各节点的值均保证唯一。
思路
中序遍历最简单
代码
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
stack<TreeNode*> st;
TreeNode *prev = nullptr, *curr = root;
while (!st.empty() || curr != nullptr) {
while (curr != nullptr) {
st.emplace(curr);
curr = curr->left;
}
curr = st.top();
st.pop();
if (prev == p) {
return curr;
}
prev = curr;
curr = curr->right;
}
return nullptr;
}
};
286. 墙与门
题干
你被给定一个 m × n 的二维网格 rooms ,网格中有以下三种可能的初始化值:
-1表示墙或是障碍物0表示一扇门INF无限表示一个空的房间。然后,我们用231 - 1 = 2147483647代表INF。你可以认为通往门的距离总是小于2147483647的。
你要给每个空房间位上填上该房间到 最近门的距离 ,如果无法到达门,则填 INF 即可。
示例 1:
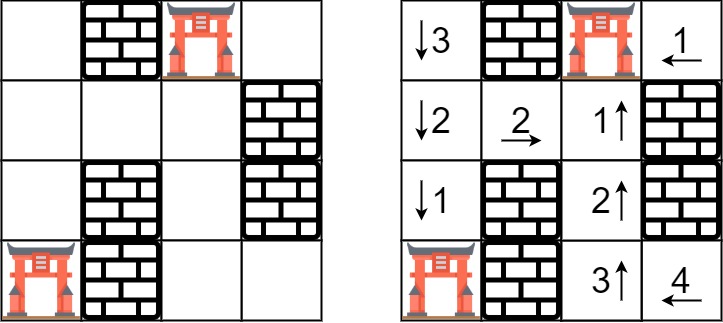
输入:rooms = [[2147483647,-1,0,2147483647],[2147483647,2147483647,2147483647,-1],[2147483647,-1,2147483647,-1],[0,-1,2147483647,2147483647]]
输出:[[3,-1,0,1],[2,2,1,-1],[1,-1,2,-1],[0,-1,3,4]]
示例 2:
输入:rooms = [[-1]]
输出:[[-1]]
示例 3:
输入:rooms = [[2147483647]]
输出:[[2147483647]]
示例 4:
输入:rooms = [[0]]
输出:[[0]]
提示:
m == rooms.lengthn == rooms[i].length1 <= m, n <= 250rooms[i][j]是-1、0或231 - 1
思路
从各个door开始bfs
代码
class Solution {
private:
const int WALL = -1;
const int DOOR = 0;
const int INF = 2147483647;
// 上下左右
int direct[4][2] ={
{1, 0},
{-1, 0},
{0, -1},
{0, 1},
};
// 队列存放节点
queue<pair<int, int>> q;
public:
void wallsAndGates(vector<vector<int>>& rooms)
{
int m = rooms.size();
if (!m) return;
int n = rooms[0].size();
if (!n) return;
// 存放DOOR位置,即多源头BFS的起点
for (int i = 0; i < m; ++i)
{
for (int j = 0; j < n; ++j)
{
if (rooms[i][j] == DOOR) q.emplace(make_pair(i, j));
}
}
while (!q.empty())
{
auto top = q.front();
q.pop();
int row = top.first;
int col = top.second;
for (int i = 0; i < 4; ++i)
{
int newRow = row + direct[i][0];
int newCol = col + direct[i][1];
if (newRow < 0 || newRow >= m || newCol < 0 || newCol >= n || rooms[newRow][newCol] != INF) continue;
rooms[newRow][newCol] = rooms[row][col] + 1;
q.emplace(make_pair(newRow, newCol));
}
}
}
};
287. 寻找重复数
题干
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
示例 1:
输入:nums = [1,3,4,2,2]
输出:2
示例 2:
输入:nums = [3,1,3,4,2]
输出:3
示例 3 :
输入:nums = [3,3,3,3,3]
输出:3
提示:
1 <= n <= 105nums.length == n + 11 <= nums[i] <= nnums中 只有一个整数 出现 两次或多次 ,其余整数均只出现 一次
进阶:
- 如何证明
nums中至少存在一个重复的数字? - 你可以设计一个线性级时间复杂度
O(n)的解决方案吗?
思路
快慢指针Floyd 判圈算法
代码
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int slow = 0, fast = 0;
do {
slow = nums[slow];
fast = nums[nums[fast]];
} while (slow != fast);
slow = 0;
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};
288. 单词的唯一缩写
题干
单词的 缩写 需要遵循 <起始字母><中间字母数><结尾字母> 这样的格式。如果单词只有两个字符,那么它就是它自身的 缩写 。
以下是一些单词缩写的范例:
dog --> d1g因为第一个字母'd'和最后一个字母'g'之间有1个字母internationalization --> i18n因为第一个字母'i'和最后一个字母'n'之间有18个字母it --> it单词只有两个字符,它就是它自身的 缩写
实现 ValidWordAbbr 类:
ValidWordAbbr(String[] dictionary)使用单词字典dictionary初始化对象boolean isUnique(string word)如果满足下述任意一个条件,返回
true;否则,返回
false:
- 字典
dictionary中没有任何其他单词的 缩写 与该单词word的 缩写 相同。 - 字典
dictionary中的所有 缩写 与该单词word的 缩写 相同的单词都与word相同 。
- 字典
示例:
输入
["ValidWordAbbr", "isUnique", "isUnique", "isUnique", "isUnique", "isUnique"]
[[["deer", "door", "cake", "card"]], ["dear"], ["cart"], ["cane"], ["make"], ["cake"]]
输出
[null, false, true, false, true, true]
解释
ValidWordAbbr validWordAbbr = new ValidWordAbbr(["deer", "door", "cake", "card"]);
validWordAbbr.isUnique("dear"); // 返回 false,字典中的 "deer" 与输入 "dear" 的缩写都是 "d2r",但这两个单词不相同
validWordAbbr.isUnique("cart"); // 返回 true,字典中不存在缩写为 "c2t" 的单词
validWordAbbr.isUnique("cane"); // 返回 false,字典中的 "cake" 与输入 "cane" 的缩写都是 "c2e",但这两个单词不相同
validWordAbbr.isUnique("make"); // 返回 true,字典中不存在缩写为 "m2e" 的单词
validWordAbbr.isUnique("cake"); // 返回 true,因为 "cake" 已经存在于字典中,并且字典中没有其他缩写为 "c2e" 的单词
提示:
1 <= dictionary.length <= 3 * 1041 <= dictionary[i].length <= 20dictionary[i]由小写英文字母组成1 <= word <= 20word由小写英文字母组成- 最多调用
5000次isUnique
思路
两个哈希表,一个存单词数量,一个存make修改后的缩写数量
代码
class ValidWordAbbr {
unordered_map<string, int> ts, ss;
string make(string& x){
return x.size() <= 2 ? x : x.front() + to_string(x.size() - 2) + x.back();
}
public:
ValidWordAbbr(vector<string>& dictionary) {
for(auto&& x: dictionary) ++ts[x], ++ss[make(x)];
}
bool isUnique(string word) {
auto y = make(word);
return (ts.count(word) ? ts[word] : 0) == (ss.count(y) ? ss[y] : 0);
}
};
/**
* Your ValidWordAbbr object will be instantiated and called as such:
* ValidWordAbbr* obj = new ValidWordAbbr(dictionary);
* bool param_1 = obj->isUnique(word);
*/
289. 生命游戏
题干
根据 百度百科 , 生命游戏 ,简称为 生命 ,是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。
给定一个包含 m × n 个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态: 1 即为 活细胞 (live),或 0 即为 死细胞 (dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态,返回下一个状态。
示例 1:
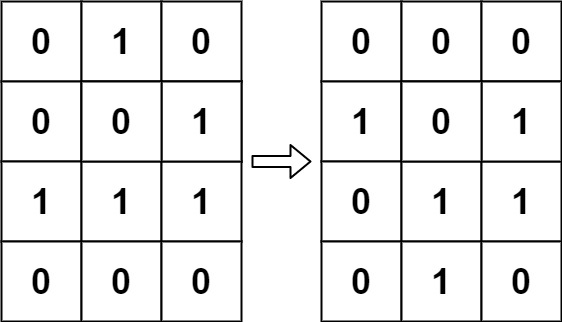
输入:board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]
示例 2:
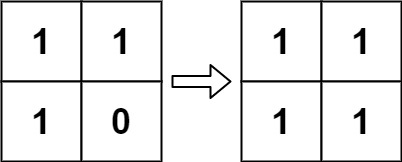
输入:board = [[1,1],[1,0]]
输出:[[1,1],[1,1]]
提示:
m == board.lengthn == board[i].length1 <= m, n <= 25board[i][j]为0或1
进阶:
- 你可以使用原地算法解决本题吗?请注意,面板上所有格子需要同时被更新:你不能先更新某些格子,然后使用它们的更新后的值再更新其他格子。
- 本题中,我们使用二维数组来表示面板。原则上,面板是无限的,但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题?
思路
最简单每次额外空间存每轮结果,更省空间的方法是位运算,把下一轮结果以位运算的方式存下来
代码
class Solution {
public:
void gameOfLife(vector<vector<int>>& board) {
int dx[] = {-1, 0, 1, -1, 1, -1, 0, 1};
int dy[] = {-1, -1, -1, 0, 0, 1, 1, 1};
for(int i = 0; i < board.size(); i++) {
for(int j = 0 ; j < board[0].size(); j++) {
int sum = 0;
for(int k = 0; k < 8; k++) {
int nx = i + dx[k];
int ny = j + dy[k];
if(nx >= 0 && nx < board.size() && ny >= 0 && ny < board[0].size()) {
sum += (board[nx][ny]&1); // 只累加最低位
}
}
if(board[i][j] == 1) {
if(sum == 2 || sum == 3) {
board[i][j] |= 2; // 使用第二个bit标记是否存活
}
} else {
if(sum == 3) {
board[i][j] |= 2; // 使用第二个bit标记是否存活
}
}
}
}
for(int i = 0; i < board.size(); i++) {
for(int j = 0; j < board[i].size(); j++) {
board[i][j] >>= 1; //右移一位,用第二bit覆盖第一个bit。
}
}
}
};
291. 单词规律 II
题干
给你一种规律 pattern 和一个字符串 s,请你判断 s 是否和 pattern 的规律相匹配。
如果存在单个字符到 非空 字符串的 双射映射 ,那么字符串 s 匹配 pattern ,即:如果 pattern 中的每个字符都被它映射到的字符串替换,那么最终的字符串则为 s 。双射 意味着映射双方一一对应,不会存在两个字符映射到同一个字符串,也不会存在一个字符分别映射到两个不同的字符串。
示例 1:
输入:pattern = "abab", s = "redblueredblue"
输出:true
解释:一种可能的映射如下:
'a' -> "red"
'b' -> "blue"
示例 2:
输入:pattern = "aaaa", s = "asdasdasdasd"
输出:true
解释:一种可能的映射如下:
'a' -> "asd"
示例 3:
输入:pattern = "aabb", s = "xyzabcxzyabc"
输出:false
提示:
1 <= pattern.length, s.length <= 20pattern和s由小写英文字母组成
思路
记忆化搜索dfs
代码
class Solution {
public:
bool wordPatternMatch(string pattern, string s) {
unordered_map<char,string> mp;
unordered_map<string,char> mp2;
int n = pattern.size();
int m = s.size();
bool answer = false;
function<void(int,int)> dfs = [&](int i,int j){
if(answer==true){
return;
}
if(i==n&&j==m){
answer = true;
return;
}
if(i==n||j==m){
return;
}
char now = pattern[i];
if(mp.count(now)){
if(mp[now]==s.substr(j,mp[now].size())){
dfs(i+1,j+mp[now].size());
}
}else{
for(int k=1;k<=m-j;k++){
if(mp2.count(s.substr(j,k))==0){
mp[now] = s.substr(j,k);
mp2[s.substr(j,k)] = now;
dfs(i+1,j+k);
mp.erase(now);
mp2.erase(s.substr(j,k));
}
}
}
};
dfs(0,0);
return answer;
};
};
294. 翻转游戏 II
题干
你和朋友玩一个叫做「翻转游戏」的游戏。游戏规则如下:
给你一个字符串 currentState ,其中只含 '+' 和 '-' 。你和朋友轮流将 连续 的两个 "++" 反转成 "--" 。当一方无法进行有效的翻转时便意味着游戏结束,则另一方获胜。默认每个人都会采取最优策略。
请你写出一个函数来判定起始玩家 是否存在必胜的方案 :如果存在,返回 true ;否则,返回 false 。
示例 1:
输入:currentState = "++++"
输出:true
解释:起始玩家可将中间的 "++" 翻转变为 "+--+" 从而得胜。
示例 2:
输入:currentState = "+"
输出:false
提示:
1 <= currentState.length <= 60currentState[i]不是'+'就是'-'
进阶:请推导你算法的时间复杂度。
思路
暴力回溯
代码
class Solution {
public:
bool canWin(string currentState)
{ //回溯
string s = currentState; //纯粹为了好写
int n = s.size();
for (int i = 0; i < n - 1; i ++)
{
if (s[i] == '+' && s[i+1] == '+')
{
s[i] = '-';
s[i+1] = '-';
if (canWin (s) == false)
return true;
s[i] = '+'; //回溯,有借有还
s[i+1] = '+'; //回溯,有借有还
}
}
return false;
}
};
298. 二叉树最长连续序列
题干
给你一棵指定的二叉树的根节点 root ,请你计算其中 最长连续序列路径 的长度。
最长连续序列路径 是依次递增 1 的路径。该路径,可以是从某个初始节点到树中任意节点,通过「父 - 子」关系连接而产生的任意路径。且必须从父节点到子节点,反过来是不可以的。
示例 1:
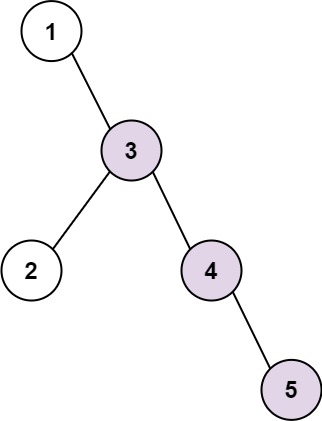
输入:root = [1,null,3,2,4,null,null,null,5]
输出:3
解释:当中,最长连续序列是 3-4-5 ,所以返回结果为 3 。
示例 2:
输入:root = [2,null,3,2,null,1]
输出:2
解释:当中,最长连续序列是 2-3 。注意,不是 3-2-1,所以返回 2 。
提示:
- 树中节点的数目在范围
[1, 3 * 104]内 -3 * 104 <= Node.val <= 3 * 104
思路
树的dfs题
代码
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int longestConsecutive(TreeNode* root) {
int answer = 1;
function<int(TreeNode*)> dfs = [&](TreeNode* root){
if(!root->left&&!root->right){
return 1;
}
int num = 1;
int temp = 0;
int temp2 = 0;
if(root->left){
temp=dfs(root->left);
if(root->val+1==root->left->val){
num = max(num,1+temp);
}
}
if(root->right){
temp2 = dfs(root->right);
if(root->val+1==root->right->val){
num = max(num,1+temp2);
}
};
//cout<<root->val<<" "<<num<<" "<<temp<<" "<<temp2<<endl;
answer = max(num,answer);
return num;
};
dfs(root);
return answer;
}
};
299. 猜数字游戏
题干
你在和朋友一起玩 猜数字(Bulls and Cows)游戏,该游戏规则如下:
写出一个秘密数字,并请朋友猜这个数字是多少。朋友每猜测一次,你就会给他一个包含下述信息的提示:
- 猜测数字中有多少位属于数字和确切位置都猜对了(称为 “Bulls”,公牛),
- 有多少位属于数字猜对了但是位置不对(称为 “Cows”,奶牛)。也就是说,这次猜测中有多少位非公牛数字可以通过重新排列转换成公牛数字。
给你一个秘密数字 secret 和朋友猜测的数字 guess ,请你返回对朋友这次猜测的提示。
提示的格式为 "xAyB" ,x 是公牛个数, y 是奶牛个数,A 表示公牛,B 表示奶牛。
请注意秘密数字和朋友猜测的数字都可能含有重复数字。
示例 1:
输入:secret = "1807", guess = "7810"
输出:"1A3B"
解释:数字和位置都对(公牛)用 '|' 连接,数字猜对位置不对(奶牛)的采用斜体加粗标识。
"1807"
|
"7810"
示例 2:
输入:secret = "1123", guess = "0111"
输出:"1A1B"
解释:数字和位置都对(公牛)用 '|' 连接,数字猜对位置不对(奶牛)的采用斜体加粗标识。
"1123" "1123"
| or |
"0111" "0111"
注意,两个不匹配的 1 中,只有一个会算作奶牛(数字猜对位置不对)。通过重新排列非公牛数字,其中仅有一个 1 可以成为公牛数字。
提示:
1 <= secret.length, guess.length <= 1000secret.length == guess.lengthsecret和guess仅由数字组成
思路
按照题意遍历模拟
代码
class Solution {
public:
string getHint(string secret, string guess) {
int bulls = 0;
vector<int> cntS(10), cntG(10);
for (int i = 0; i < secret.length(); ++i) {
if (secret[i] == guess[i]) {
++bulls;
} else {
++cntS[secret[i] - '0'];
++cntG[guess[i] - '0'];
}
}
int cows = 0;
for (int i = 0; i < 10; ++i) {
cows += min(cntS[i], cntG[i]);
}
return to_string(bulls) + "A" + to_string(cows) + "B";
}
};
300. 最长递增子序列
题干
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的
子序列
。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3]
输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7]
输出:1
提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
进阶:
- 你能将算法的时间复杂度降低到
O(n log(n))吗?
思路
LIS问题的动态规划很好想,但是时间复杂度可能超时,本题可以贪心加二分查找,具体来说维护一个变长数组,每个位置i表示长度为i+1的上升子串当前的末尾值,对于一个新的数进这个数组来说,如果其比当前数组末尾要大就直接加末尾,否则替换找到第一个比 nums[i]小的数 d[k] ,并更新 d[k+1]=nums[i]
代码
//动态规划
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int n = (int)nums.size();
if (n == 0) {
return 0;
}
vector<int> dp(n, 0);
for (int i = 0; i < n; ++i) {
dp[i] = 1;
for (int j = 0; j < i; ++j) {
if (nums[j] < nums[i]) {
dp[i] = max(dp[i], dp[j] + 1);
}
}
}
return *max_element(dp.begin(), dp.end());
}
};
//贪心
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int len = 1, n = (int)nums.size();
if (n == 0) {
return 0;
}
vector<int> d(n + 1, 0);
d[len] = nums[0];
for (int i = 1; i < n; ++i) {
if (nums[i] > d[len]) {
d[++len] = nums[i];
} else {
int l = 1, r = len, pos = 0; // 如果找不到说明所有的数都比 nums[i] 大,此时要更新 d[1],所以这里将 pos 设为 0
while (l <= r) {
int mid = (l + r) >> 1;
if (d[mid] < nums[i]) {
pos = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
d[pos + 1] = nums[i];
}
}
return len;
}
};